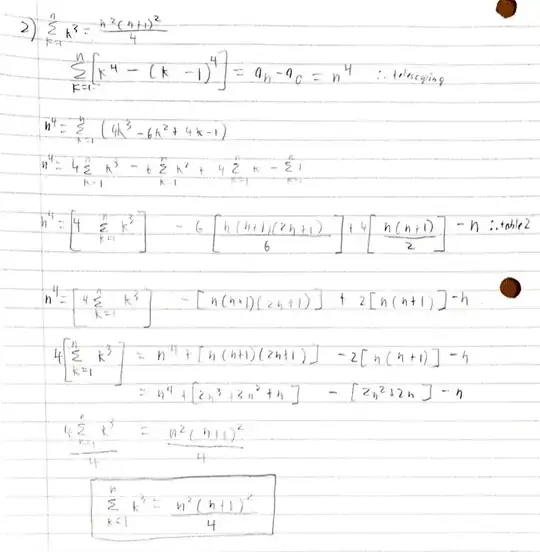1

I know how to do this problem when trying to get sum of squares

$$\Sigma k^2 = n(n+1)(2n+1)/ 6 $$

But I’m having trouble proving for cubes:

$$\sum_{k=1}^n k^3 = \frac{n^2(n+1)^2}4$$

I have to prove this by the method of telescopy.

Edit $ $ Below is my attempt based on discussion on an answer below

I started by writing $\ \displaystyle \sum_{k=1}^n (k^4-(k-1)^4) = n^4.$

but I don't know where to go once I get here $\ \displaystyle \sum_{k=1}^n (4k^3-6k^2+4k-1) = n^4 $

I used a table in a book for the others but I don't know how to convert the first summand $\ 4 \sum_{k=1}^n k^3$ to complete the proof.

Update $\ $ If anyone is interested in the exact solution I posted an answer showing what I did.

quid
  • 42,135
CTOverton
  • 219

4 Answers4

3

The proof reduces to simple polynomial arithmetic if you apply the telescopy theorem below, viz.

$$ \overbrace{\dfrac{n^2(n+1)^2}4}^{\Large F(n)}\, =\, \sum_{k\: =\: 1}^n\:\overbrace{k^3}^{\Large f(k)} \iff \ \color{#c00}{F(1)=f(1)},\,\ \ F(n) - F(n\!-\!1)\ =\ f(n)\ \ {\rm for}\ \ n> 1$$

Checking: the base equation: $\color{#c00}{F(1)} = 1^2 2^2/4 = 1 = 1^3 = \color{#c00}{f(1)}\,$ is true, as is the inductive equation

$$F(n)-F(n-1)\, =\, \dfrac{n^2(n+1)^2}4 - \dfrac{n^2(n-1)^2}4 = \dfrac{n^2(4n)}4 = n^3 = f(n)$$

That completes the proof by the Theorem below.

Theorem $\ $ (Additive Telescopic Induction)

$$ F(n)\ =\, \sum_{\large k\: =\: 1}^{\large n}\:\ f(k)\ \ \iff\ \ \ \color{#c00}{F(1)=f(1)},\,\ \ F(n) - F(n\!-\!1)\ =\ f(n)\ \ {\rm for}\ \ n> 1$$

Proof $\ (\Leftarrow)\ $ The $\,n=1\,$ base case $\,\color{#c00}{F(1) = f(1)} = \sum_{k=1}^1 f(k)\,$ is true, as is the inductive step:

$$\begin{align} F(n\!+\!1)\ &=\ \ \color{#0a0}{F(n)}\ \ +\ f(n\!+\!1)\ \ \ {\rm by\ hypothesis}\\ &=\, \color{#0a0}{\sum_{i=1}^n f(i)} + f(n\!+\!1)\ \ \ {\rm by\ }\color{#0a0}{\rm induction}\\ &=\, \sum_{i=1}^{n+1} f(i) \end{align}$$

That proves the nontrivial direction $(\Leftarrow)$. The reverse direction is clear. $\ $ QED

Remark $ $ Note that the proof requires no ingenuity whatsoever. Rather it requires only simple computations that are so mechanical that they can be performed by a computer (namely equality testing of polynomials). In particular there is no need to pull your hair out in search of the appropriate inductive step - that is neatly encapsulated once and for all in the Theorem.

See this post and its links for much further discussion of telescopy.

Bill Dubuque
  • 272,048
2

Note that $$ (k+1)^2k^2 - k^2(k-1)^2 = k^2[(k+1)^2 - (k-1)^2] = k^2[(2k)\cdot (2)] = 4k^3. $$

Hence, $$ 4 \sum_{k = 0}^n k^3 = (n+1)^2n^2 $$ as wanted.

Hugo
  • 1,609
2

If anyone is interested in the exact solution here is what I did:

Solution

CTOverton
  • 219
  • 1
    Consider using Mathjax to format your answer. – Akira Oct 02 '18 at 01:03
  • @Akira thank you I was trying to figure that out – CTOverton Oct 02 '18 at 01:23
  • You're welcome! – Akira Oct 02 '18 at 01:54
  • The method you used above is not what most would call a telescopic proof of the given sum. So if that's what your instructor requested then you may want to double check on that. The standard proof by telescopy is the one mentioned in my answer. That does not require doing any other sums. – Bill Dubuque Oct 09 '18 at 03:32
1

Hint: If you already have an expression for the sum of consecutive squares then try playing with $\sum_{k=1}^n (k^4-(k-1)^4) = n^4.$

user328442
  • 2,705
  • I actually was going to put that in my question. That's where I started but I don't know where to go once I get here n∑k=1 (4k^3-6k^2+4k-1) = n^4 – CTOverton Oct 01 '18 at 23:50
  • 1
    @CTOverton notice that you have $4 \cdot \sum_{k=1}^n k^3 -6 \cdot \sum_{k=1}^n k^2 + 4 \cdot \sum_{k=1}^n k - \sum_{k=1}^n 1.$ – user328442 Oct 02 '18 at 00:03
  • Yes, I get there and I get all the summations into n form, except the first one. I used a table in a book for the others but I don't know how to convert the first one... the 4*∑nk=1k3 – CTOverton Oct 02 '18 at 00:06
  • 1
    @CTOverton you just solve for $\sum_{k=1}^n k^3.$ The right-hand side of the equation is $n^4$ and the left-hand side of the equation has a bunch of expressions in terms of n aside from the sum of cubes... – user328442 Oct 02 '18 at 00:09
  • does the answer I posted look correct? Thanks again really helped! – CTOverton Oct 02 '18 at 00:34
  • 1
    @CTOverton it looks correct to me. That is what I was leading to. – user328442 Oct 02 '18 at 00:40
  • @CTOverton You don't need to know any closed forms for sums of squares to verify it by telescopy - see my answer. – Bill Dubuque Oct 04 '18 at 00:01