1

Preliminary: One reason that in the (algebro-geometric) theory of $\mathbb{Q}$ arbitrary powers $p^q$ are not considered is, that there is no finite Euclidean construction which would yield $p^q$ for arbitrary lengths $p$ and $q$. This already and most prominently holds for $q = \frac{1}{3}$: While $\sqrt[2]{p}$ can be constructed, $\sqrt[3]{p}$ can not.

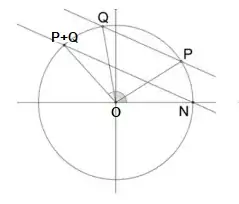
On the unit circle the sum of two angles $\alpha = \angle NOP$ and $\beta = \angle NOQ$ (= two arc lengths $\overline{NP}$, $\overline{NQ}$) can be constructed:

enter image description here

which - by the way - has a strong similarity (by the use of parallels) with the multiplication of straight lengths:

enter image description here

It turns out that the addition of (arc) lengths on the circle corresponds to the multiplication of two Gaussian numbers in the plane $\mathbb{Q}(i)$: $\alpha \oplus \beta := e^{i\alpha} \cdot e^{i\beta} = e^{i(\alpha + \beta)} $.

If it were possible to unroll the circle onto the straight line, we could add two angles (= arc length) as straight line segments and roll the sum back onto the circle (modulo $2\pi$). Even though unrolling is not possible (by Euclidean constructions), addition of angles is possible (taking something like a magic shortcut, see above).

What would the multiplication of arc lengths on the circle correspond to? If unrolling were possible we could multiply angles in the same way that we add them: unroll the arc lengths $\alpha, \beta$ onto the straight line, multiply them here (see above) and roll the product back onto the circle (modulo $2\pi$).

How can it be seen that there is no "magic geometric shortcut" - as in the case of addition - that yields the product of two arbitrary angles modulo $2\pi$?

The only (?) way we can construct multiplication on the unit circle is by restricting the numbers/points/angles/arc lengths to some roots of unity $\omega_m^n = e^{i2\pi n/m}$. We then can multiply two numbers by $\omega_m^p \otimes \omega_m^q := \omega_m^q \oplus \dots \oplus \omega_m^q = \omega_m^{pq}$.

Hans-Peter Stricker
  • 18,159
  • Related: Powers of circular arc-lengths can be seen in involutes, which are approximated by a straightforward construction. This answer of mine discusses how this leads to a geometric interpretation of the power series of sine, cosine, tangent, and secant. (Cotangent and cosecant still elude me.) – Blue Oct 02 '18 at 14:39

1 Answers1

1

An obvious question is this: it seems the point $N$ on the circle in the first figure is meant to correspond to the point labeled $0$ in the second figures; but which point on the circle will correspond to $1$ when you make your theory of multiplication of angles?

The thing about the geometric multiplication of lengths is that the choice of unit length is generally considered arbitrary, at least in relation to classical geometry. Using the symbols $0$ and $1$ as the names of points on the line $PQ$ rather than as numbers, the construction finds a point $R$ (labeled $P\cdot Q$ in the figure) such that the lengths of the segments $01,$ $0P,$ $0Q,$ and $0R$ are in the proportion $$ \lvert 01 \rvert : \lvert 0P \rvert = \lvert 0Q \rvert : \lvert 0R \rvert.$$

This is a powerful tool. Among other things, it lets us divide any segment exactly in three equal parts. Here's how: given the points $0,$ $1,$ and $P,$ put $Q$ at an arbitrary distance to the right of $P,$ construct a point $R$ even farther to the right such that $\lvert 0R \rvert = 3\lvert 0Q \rvert,$ and relabel the point $R$ as $P\cdot Q.$ We then construct something much like the second figure using parallel lines, except that the oblique line through $P$ intersects the vertical line at a point we label $P/R$ and the second oblique line through $P/R$ intersects the line $PQ$ at a point we label $P/3.$

We know for certain there is no such powerful method for making proportional angles via a classical construction, because that method would provide a classical method for trisecting general angles and we know that no such method can exist.

David K
  • 98,388