3

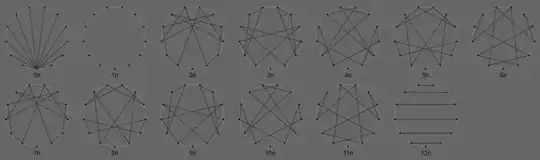
The multiplication graphs for $\mathbb{Z}_p := \mathbb{Z}/p\mathbb{Z}$ (with $p$ prime) visually reveal some basic facts, especially that each non-zero element has an inverse, or – equivalently – that they have no zero divisors, or – equivalently – that $\mathbb{Z}_p$ is a field.

These are the multiplication graphs for $\mathbb{Z}_{13}$:

enter image description here

What they also reveal is that the units $\mathbb{Z}_p^\times$, i.e. the non-zero elements of $\mathbb{Z}_p$, form a group: For each $m \neq 0$ the function $\pi_m: n \mapsto m\cdot n$ is a permutation of $\mathbb{Z}_p^\times$. You see immediately that $\pi_1 = \text{id}$ and that $\pi_{p-1}\pi_{p-1} = \text{id}$. You can also check easily that $\pi_{mn} = \pi_{m}\pi_n$, and that $\pi_{m}\pi_n = \pi_1$ iff $mn \equiv 1\mod p$.

My question is:

Does the group of units of $\mathbb{Z}_p$ – considered as a subgroup of the symmetric group $S_{p-1}$ (that's what it "is" and how it can be visualized) – have a proper name: the XY group of $p$? Or is "the group of units of $\mathbb{Z}_p$" all that there is?

[Edit: From lhf's answer I've learned that the proper name is "the cyclic group of order $p-1$".]

Furthermore: How can you tell the structure of this group from $p$? Which properties of the group can you tell from $p$? (I guess not so many, because $p$ is prime, has no factors and thus has not many properties that could give rise to properties of the group.)

Edit: One characteristic of a permutation group is its permutation type spectrum. To ask the last question more specifically: Can you tell the permutation type spectrum of $\mathbb{Z}_p^\times$ from $p$ without writing all the permutations down?

The permutation type spectrum of $\mathbb{Z}_{13}^\times$ is

$$[12^1]^4[6^2]^2[4^3]^2[3^4]^2[2^6]^1[1^{12}]^1$$

As an example here is the complete group for $p = 13$:

$\pi_2=(\ \ 1\ \ 2\ \ 4\ \ 8\ \ 3\ \ 6\ \ 12\ \ 11\ \ 9\ \ 5\ \ 10\ \ 7\ \ )$

$\pi_3=(\ \ 1\ \ 3\ \ 9\ \ )\ \ (\ \ 2\ \ 6\ \ 5\ \ )\ \ (\ \ 4\ \ 12\ \ 10\ \ )\ \ (\ \ 7\ \ 8\ \ 11\ \ )$

$\pi_4=(\ \ 1\ \ 4\ \ 3\ \ 12\ \ 9\ \ 10\ \ )\ \ (\ \ 2\ \ 8\ \ 6\ \ 11\ \ 5\ \ 7\ \ )\ \ $

$\pi_5=(\ \ 1\ \ 5\ \ 12\ \ 8\ \ )\ \ (\ \ 2\ \ 10\ \ 11\ \ 3\ \ )\ \ (\ \ 4\ \ 7\ \ 9\ \ 6\ \ )$

$\pi_6=(\ \ 1\ \ 6\ \ 10\ \ 8\ \ 9\ \ 2\ \ 12\ \ 7\ \ 3\ \ 5\ \ 4\ \ 11\ \ )\ \ $

$\pi_7=(\ \ 1\ \ 7\ \ 10\ \ 5\ \ 9\ \ 11\ \ 12\ \ 6\ \ 3\ \ 8\ \ 4\ \ 2\ \ )\ \ $

$\pi_8=(\ \ 1\ \ 8\ \ 12\ \ 5\ \ )\ \ (\ \ 2\ \ 3\ \ 11\ \ 10\ \ )\ \ (\ \ 4\ \ 6\ \ 9\ \ 7\ \ )\ \ $

$\pi_9=(\ \ 1\ \ 9\ \ 3\ \ )\ \ (\ \ 2\ \ 5\ \ 6\ \ )\ \ (\ \ 4\ \ 10\ \ 12\ \ )\ \ (\ \ 7\ \ 11\ \ 8\ \ )$

$\pi_{10}=(\ \ 1\ \ 10\ \ 9\ \ 12\ \ 3\ \ 4\ \ )\ \ (\ \ 2\ \ 7\ \ 5\ \ 11\ \ 6\ \ 8\ \ )$

$\pi_{11}=(\ \ 1\ \ 11\ \ 4\ \ 5\ \ 3\ \ 7\ \ 12\ \ 2\ \ 9\ \ 8\ \ 10\ \ 6\ \ )\ \ $

$\pi_{12}=(\ \ 1\ \ 12\ \ )\ \ (\ \ 2\ \ 11\ \ )\ \ (\ \ 3\ \ 10\ \ )\ \ (\ \ 4\ \ 9\ \ )\ \ (\ \ 5\ \ 8\ \ )\ \ (\ \ 6\ \ 7\ \ )$

Note that you can literally see the "cycle structure" of each permutation in the corresponding graph.

Does this specific permutation group have a canonical name?

For the sake of completeness here is the multiplication table for the same group considered as a group of numbers (not permutations):

$$\begin{array}{c||c|c|c|c|c|c|c|c|c|c|c|c} & 1 & 2 & 3 & 4 & 5 & 6 & 7 & 8 & 9 & 10 & 11 & 12 \\ \hline 1 & 1 & 2 & 3 & 4 & 5 & 6 & 7 & 8 & 9 & 10 & 11 & 12 \\ \hline 2 & 2 & 4 & 6 & 8 & 10 & 12 & 1 & 3 & 5 & 7 & 9 & 11 \\ \hline 3 & 3 & 6 & 9 & 12 & 2 & 5 & 8 & 11 & 1 & 4 & 7 & 10 \\ \hline 4 & 4 & 8 & 12 & 3 & 7 & 11 & 2 & 6 & 10 & 1 & 5 & 9 \\ \hline 5 & 5 & 10 & 2 & 7 & 12 & 4 & 9 & 1 & 6 & 11 & 3 & 8 \\ \hline 6 & 6 & 12 & 5 & 11 & 4 & 10 & 3 & 9 & 2 & 8 & 1 & 7 \\ \hline 7 & 7 & 1 & 8 & 2 & 9 & 3 & 10 & 4 & 11 & 5 & 12 & 6 \\ \hline 8 & 8 & 3 & 11 & 6 & 1 & 9 & 4 & 12 & 7 & 2 & 10 & 5 \\ \hline 9 & 9 & 5 & 1 & 10 & 6 & 2 & 11 & 7 & 3 & 12 & 8 & 4 \\ \hline 10 & 10 & 7 & 4 & 1 & 11 & 8 & 5 & 2 & 12 & 9 & 6 & 3 \\ \hline 11 & 11 & 9 & 7 & 5 & 3 & 1 & 12 & 10 & 8 & 6 & 4 & 2 \\ \hline 12 & 12 & 11 & 10 & 9 & 8 & 7 & 6 & 5 & 4 & 3 & 2 & 1 \\ \end{array}$$

Note that you can see almost nothing here (except at the borders of the square).

Hans-Peter Stricker
  • 18,159
  • 1
    I suggest you ask a separate question about the permutation spectrum. The answer is simple, though: For each divisor $d$ of $p-1$, there are $\phi(d)$ permutations with $(p-1)/d$ $d$-cycles. – lhf Nov 13 '18 at 12:20
  • That's simple enough! Also the proof? – Hans-Peter Stricker Nov 13 '18 at 12:29
  • There are exactly $\phi(d)$ elements of order $d$ in a cyclic group of order $n$. These elements generated a subgroup of order $d$ and so with index $n/d$. – lhf Nov 13 '18 at 12:31
  • I'd say $\mathbb{Z}/p\mathbb{Z}$ is cyclic of order $p$, $\mathbb{Z}/p\mathbb{Z}^\times$ is cyclic of order $p-1$ (two very simple structures), the complicated structure arise in the ring $\mathbb{Z}/p\mathbb{Z},+,\times$ where the two cyclic groups are "glued together", say by identifying $\phi \in Aut(\mathbb{Z}/p\mathbb{Z})\simeq \mathbb{Z}/p\mathbb{Z}^\times$ with $\phi(1)\in \mathbb{Z}/p\mathbb{Z}$. – reuns Nov 13 '18 at 16:21

1 Answers1

1

The group of units of $\mathbb Z_p$ is always cyclic. Hence the $12$-cycles $\pi_2, \pi_6,\pi_7,\pi_{11}$ in your example.

However, no formula is known for finding $g$ such that $\pi_g$ is a $(p-1)$-cycle. Such $g$ are called primitive roots modulo $p$.

In your example, $2,6,7,11$ are the primitive roots modulo $13$.

lhf
  • 216,483