I am trying to prove the existence of $t_{0}$ such that $$\int_{0}^{t}\frac{\sin{x}}{\sqrt{x}}dx+\sin{t}>0 $$ for all $t\geq t_{0}$.
Numerical experiments shows this (see the figure).
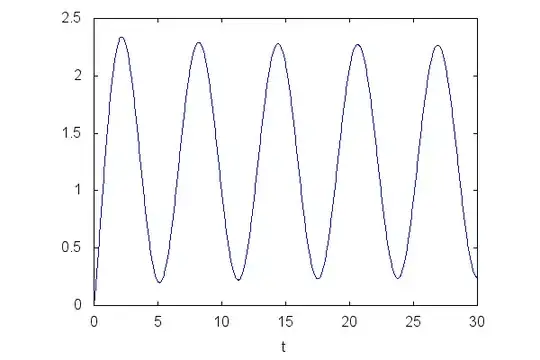
The first thing that may come to mind is to show the existence of $t_{0}$ such that $$\int_{0}^{t}\frac{\sin{x}}{\sqrt{x}}dx>1 $$ when $t\geq t_{0}$
The full (improper Riemann) integral on the half line is well known, see Proof of $\int_0^\infty \frac{\sin x}{\sqrt{x}}dx=\sqrt{\frac{\pi}{2}}$ . (A very related term to google : Fresnel integral.) The definition of having a finite limit as $t\to\infty$ immediately gives the existence of some $t_0>0$ such that if $t>t_0$,
$$\left| \int_0^t \frac{\sin x}{\sqrt x}\ dx - \sqrt{\frac{\pi}{2}} \right| < 0.1. $$
As $\sqrt{\pi/2} > 1.2$, $\int_0^t \frac{\sin x}{\sqrt x}\ dx > 1.1 > 1$ for $t>t_0$, as required.
Let $t>\pi$. Then
$$\left|\int_{5\pi}^{t}\frac{\sin{x}}{\sqrt{x}}dx\right|\leq \frac{1}{\sqrt{5\pi}} \left|\int_{5\pi}^{t}\sin{x}dx\right| \leq \frac{2}{\sqrt{5\pi}}=0.5046265$$
Using matlab, $$\int_{0}^{5\pi}\frac{\sin{x}}{\sqrt{x}}dx=1.5048853$$
Therefore, if $t>\pi$ then $\int_{5\pi}^{t}\frac{\sin{x}}{\sqrt{x}}dx>1$.
Now, can it be done analytically ?