Problem
How many elements are there in $\mathbb{Z}[i]/I$ where $I= \langle2+2i\rangle$
$2+2i + I =I$ . So $2+2i$ is equivalent to $0$ . So $2+2i=0$ which implies $i=-1$ which inturn implies $2=0$.
How to move after that?
Problem
How many elements are there in $\mathbb{Z}[i]/I$ where $I= \langle2+2i\rangle$
$2+2i + I =I$ . So $2+2i$ is equivalent to $0$ . So $2+2i=0$ which implies $i=-1$ which inturn implies $2=0$.
How to move after that?
Hint:
Here is a nice way to think about what $\Bbb Z[i]/I$ looks like. You are looking at elements $\alpha, \beta \in\Bbb Z[i]$ and calling them equal if you can get from one to another by adding an element from $I$. For instance, $1+2i\equiv_I 3+4i$ since $3+4i=(2+2i)+1+2i$.
To see what $(2+2i)$, the ideal, looks like you can start by plotting the point $\alpha=2+2i$. Remember that you can add anything from $(2+2i)$ to this point $\alpha$
, including:
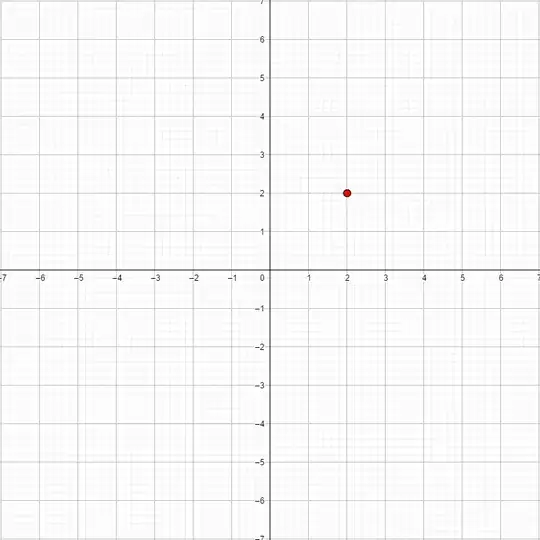
This should give you a new picture:
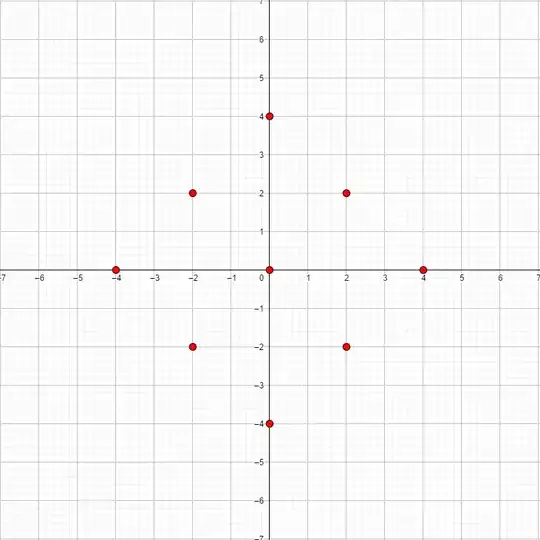
There are obviously and an infinite amount of red points, but I'm only drawing some. All these red points are infact the same element in the ring $\Bbb Z[i]/I$, so the amount of different colours needed to fill the grid is the cardinality of $\Bbb Z[i]/I$. You can continue in this way with $1+i+(2+2i)$ to get:
Another hint:
The smallest distance between two points of same colour is $\sqrt{2^2+2^2}$.
Let $f:\mathbb{Z}[i]\to \mathbb{N}, f(a+bi)=a^2+b^2 $, then $\mathbb{Z}[i]$ is an ED so $\mathbb{Z}[i]/I=\{a+bi+(2+2i): a^2+b^2<2^2+2^2=8\}$ this is because we have considered $\mathbb{Z}[i]$ as an ED so by the division algorithm we have that every element of $\dfrac{\mathbb{Z}[i]}{I}$ is of the form $(c+di)(2+2i)+x+yi$ where $x+yi=0$ or $f(a+bi)<f(2+2i)$.
We want to examine the structure of $\mathbb{Z}[i]/I$ as a $\mathbb{Z}-$module so since $\mathbb{Z}$ is a PID and $\mathbb{Z}[i]/I$ finitely generated we may use the Structure Theorem (I'm sorry but in order to give a full answer I have to use modules)
As an $\mathbb{Z}-$module $\mathbb{Z}[i]$ has basis $e=\{1,i\}$ and $a=(a+bi)\quad \{a+bi,-b+ai\}$ and so $A=(id:a,e)=\begin{pmatrix} a& -b\\ b& a\end{pmatrix}$. A smith canonical form of this matrix is $B=\begin{pmatrix} d_1& 0\\ 0& d_2\end{pmatrix}$ where $d_1=gcd(a,b)$ and $d_2=\dfrac{a^2+b^2}{d_1}$ so there are invertible matrices $Q,R\in\mathbb{Z}^{2\times 2}$ st
$$PAQ=B\Leftrightarrow (id:e,v)(id:a,e)(id:u,a)=(id:u,v)=\begin{pmatrix} d_1& 0\\ 0& d_2\end{pmatrix}$$ so
$$u_1=d_1v_1,u_2=d_2v_2$$ and $$\dfrac{\mathbb{Z}[i]}{I}\cong\dfrac{\mathbb{Z}u_1\oplus \mathbb{Z}u_2}{\mathbb{Z}d_1u_1\oplus \mathbb{Z}d_2u_2} \cong \dfrac{(u_1)}{(d_1u_1)}\oplus\dfrac{(u_2)}{(d_2u_2)}\cong \dfrac{\mathbb{Z}}{(d_1)}\oplus\dfrac{\mathbb{Z}}{(d_2)}\Rightarrow \bigg|\dfrac{\mathbb{Z}[i]}{I}\bigg|=d_1d_2=a^2+b^2=8$$