-1

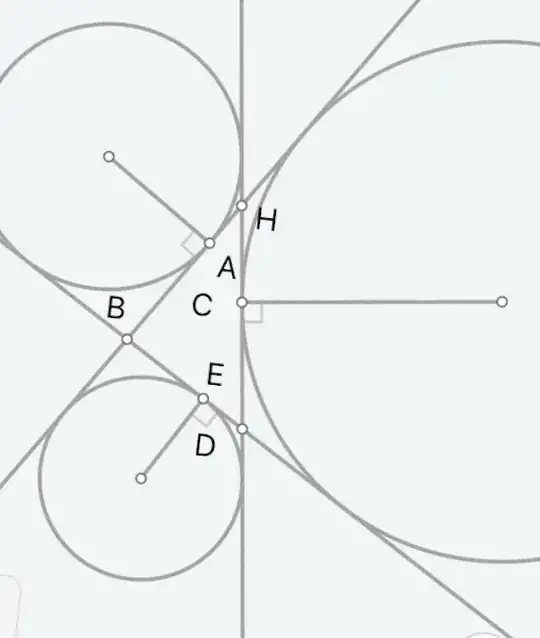
Inspired by What is the name of this theorem of Jakob Steiner's, and why is it true? enter image description here

For any triangle $HBD$, how to prove $AH = ED, \ HC = BE, \ CD = AB$?

Larry
  • 5,090
  • You'll find that simple "Here's the statement of my exercise, solve it for me" posts will be poorly received. What is better is for you to add context (with an [edit]): What you understand about the problem, what you've tried so far, etc.; something both to show you are part of the learning experience and to help us guide you to the appropriate help. You can consult this link for further guidance. – Shaun Sep 02 '18 at 14:01
  • Please try to make the titles of your questions more informative. For example, Why does $a<b$ imply $a+c<b+c$? is much more useful for other users than A question about inequality. From How can I ask a good question?: Make your title as descriptive as possible. In many cases one can actually phrase the title as the question, at least in such a way so as to be comprehensible to an expert reader. You can find more tips for choosing a good title here. – Shaun Sep 02 '18 at 14:02
  • Those vertex labels are positioned in a pretty confusing way. I'd suggest putting the labels for the triangle vertices inside of the angles opposite the triangle. Also, put the labels for the circle tangent points inside the circles (and, ideally, put them either all clockwise or all counterclockwise of the radii). – Tanner Swett Sep 02 '18 at 14:05
  • 2
    It is "known" that, along any side of the triangle, the pts of tangency of incircle and excircle are symmetric about the side's midpt. Also, tangent segments from a given pt to a given circle are congruent. Specifically, let the incircle of $\triangle ABC$ touch $\overline{BC}$, $\overline{CA}$, $\overline{AB}$ at pts $D$, $E$, $F$; let the excircles touch those edges at $D'$, $E'$, $F'$. The midpt property implies $|AF'|=|BF|$ and $|BD|=|CD'|$, and the tangent property (wrt $B$ and incircle) implies $|BF|=|BD|$. So, $|AF'|=|BF|=|BD|=|CD'|$. $\square$ (I don't know the result's name.) – Blue Sep 02 '18 at 14:26
  • @Shaun :Thanks, I will try to work through the problem harder – Larry Sep 02 '18 at 17:34

1 Answers1

1

Here's a proof that doesn't assume the midpoint property mentioned in my comment. (That property follows from what's show here, however.)

enter image description here

In $\triangle ABC$, let the side-lines through $A$ meet the excircle opposite $A$ at points $B_A$ and $C_A$. Necessarily, $|AB_A| = |AC_A|$. If that excircle meets $\overline{BC}$ at, say, $D$, then also $|BD|=|BB_A|$ and $|CD|=|CC_A|$. Consequently,

$$|AB|+|BD|=|AB|+|BB_A|=|AB_A|=|AC_A|=|AC|+|CC_A|=|AC|+|CD| \tag{1}$$

Since $|AB|+|BD|+|CD|+|AC|$ is the perimeter of $\triangle ABC$, the left- and right-most sides of $(1)$ must each equal the semi-perimeter, which we'll call $s$. In other words, $D$ is the perimeter bisector with respect to $A$. But then the point, call it $E$, where the excircle opposite $B$ touches $\overline{AC}$, is the perimeter bisector with respect to $B$. Thus, $$|BD| = s - |AB| = |AE| \tag{2}$$ which gives the result. $\square$

Blue
  • 75,673