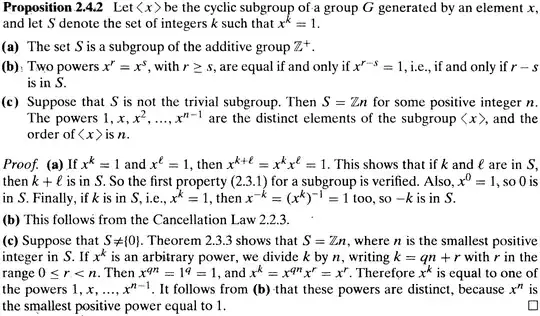1

Algebra by Michael Artin Prop 2.4.2

Here is the statement and the proof:

enter image description here

I split Prop 2.4.2(c) into Parts I, II and III respectively:

Part I: There is some positive integer $n$ s.t. $S=\mathbb Zn$

Part II: $$\langle x \rangle = \{1,x,x^2,...,x^{n-1}\}$$

Part III: order of $\langle x \rangle$ is n.

I would like to alternatively prove Part II as follows:

Pf:

By definition of $\langle x \rangle$,

$$\langle x \rangle := \{...,x^{-n}, x^{-n+1},...,x^{-2},x^{-1},1,x,x^2,...,x^{n-1},x^n,...\} \tag{1}$$

Because $S = \mathbb Zn$ (Prop 2.4.2(c) Part I), $x^n$ is killed (I think this is the term used in Chapter 3 or 11), i.e. $x^{mn}=1=x^{-mn}$ for all integers $m$, and thus elements to the right of $x^n$ and to the left of $x^{-n}$ become repeats of the ones in between them. Hence,

$$\langle x \rangle = \{... x^{-n+1},...,x^{-2},x^{-1},1, x^{-n+1},...,x^{-2},x^{-1},$$

$$1,x,x^2,...,x^{n-1},1,x,x^2,...,x^{n-1}... \} \tag{2}$$

$$ = \{ x^{-n+1},...,x^{-2},x^{-1},1,x,x^2,...,x^{n-1} \} \tag{3}$$

Now $x^n = x^{n-1}x$, whence $x^{-1}=x^{n-1}$. Similarly, $x^{-a}=x^{n-a}$ for all $a = 0,1,...,n-1$. This implies

$$\langle x \rangle = \{ 1,x,x^2,...,x^{n-1} \}. \tag{4}$$

QED

To recap:

$(1) \to (2)$: Elements beyond and including $x^n$ or $x^{-n}$ are repeats.

$(2) \to (3)$: Elements beyond and including $x^n$ or $x^{-n}$ are repeats of the ones inside.

$(3) \to (4)$: Elements with negative exponents are repeats of elements with positive exponents.

Now

$(4) \to (4)$: I just realised that I have given no reason to conclude that the representation of $\langle x \rangle$ in $(4)$ is indeed of $n$ distinct elements. If I use Part III, this is circular unless I somehow prove Part III without Part II.

How might I argue, at this stage of learning, that the elements of $\{ 1,x,x^2,...,x^{n-1} \}$ are indeed distinct besides the ways listed below?

  • Artin's $k=nq+r$.

  • Proving Part III without Part II and then using Part III to prove Part II.

'Seems no other way' is an answer.

BCLC
  • 13,459
  • 1
    I guess you need to take care about how you prove that $S=\mathbb Zn$ for some $n$. The proof is essentially proving an isomorphism with $\mathbb Zn$ for some $n$. – Mark Bennet Aug 27 '18 at 07:50
  • 1
    @MarkBennet What do you mean? $S=\mathbb Zn$ follows from (a) right? Also, how's the answer below please? Thanks! – BCLC Aug 27 '18 at 09:34
  • 2
    I mean how do you show that the only proper subgroups of $\mathbb Z$ are of the form $\mathbb Z n$? – Mark Bennet Aug 27 '18 at 13:37
  • 2
    @MarkBennet it is proved in Thm2.3.3. the proof has n=qa+r in it similar to Artin's use of k=nq+r here. Soooo....? – BCLC Aug 27 '18 at 13:42
  • 1
    So, if you want to avoid using division with remainder in the proof, you have to make sure you don't hide it in a previous theorem. – Mark Bennet Aug 27 '18 at 14:43
  • 1
    @MarkBennet why please? – BCLC Aug 27 '18 at 22:38
  • 2
    Well, if the result you want to avoid is hidden in the proof of a theorem on which you rely then you haven't really avoided it, you've just hidden it. – Mark Bennet Aug 28 '18 at 05:53
  • @MarkBennet OH I SEE. THANKS. Edited to ask about how Euclidean algorithm is not used again. – BCLC Sep 01 '18 at 13:28

1 Answers1

1

Okay, I thought of one: Not using $k=nq+r$ but has similar flavour.

Observe that $n$ is is the smallest positive integer of $S=\mathbb Zn$, i.e. $n=\min (S \cap \mathbb N \cap \{0\}^c)$. Now suppose on the contrary that there are distinct exponents $k_1, k_2$ (i.e. $k_1 \ne k_2$) in the set of $n$ exponents $\{0,1,...,n-1\}$ s.t. $x^{k_1}=x^{k_2}$. Then $x^{|k_2-k_1|}=1$, where $|k_2-k_1|$ is the absolute value of the difference of the two exponents. However, $|k_2-k_1|$ is also in $\{0,1,...,n-1\}$. This contradicts $n=\min (S \cap \mathbb N \cap \{0\}^c)$. ↯ QED

BCLC
  • 13,459