How is it that this shape can converge to what looks like a triangle but has a different perimeter?

Question

I had this strange notion some time ago, and I recently wrote a blog post about it, as a mere curiosity. I don't really consider it a "serious" mathematical question; but out of interest, I wondered if someone on this site could shed some light on what principle might be underlying the idea.

Basically, I envisioned a "pseudo-triangle" consisting of two straight edges and one jagged "edge" (not really an edge, since it's jagged, but I'm calling it that anyway):

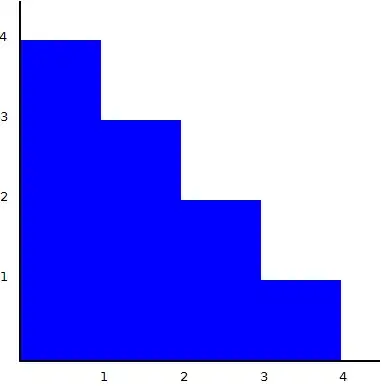
The above shape has 4 steps, its area is 10, and its perimeter is 16. Now let's increase the number of steps to 8:

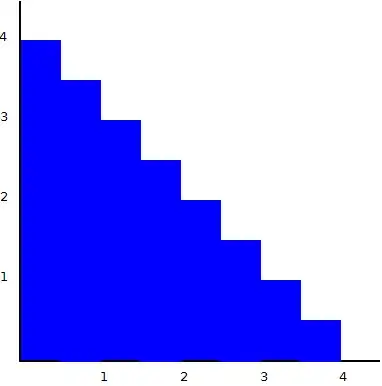
This shape has an area of 9 and a perimeter of 16. Now, without me having to write out a formal proof, I think it's pretty clear that as the number of steps increases, the area will approach 8 while the perimeter will remain constant at 16. And the resulting shape will look like this:

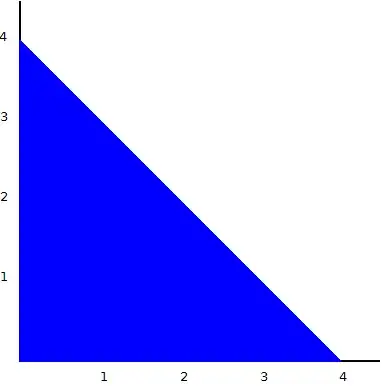
Ultimately, there's nothing really "mysterious" about this; the shape above is not a triangle, and so it shouldn't be surprising that it doesn't have quite the same properties as a triangle. However, it does approach the same area as an analogous triangle; and, more to the point, it just seems odd.

Is there a concept in mathematics that describes this phenomenon (for lack of a better word)? That is, the effect of some kind of mathematical entity (e.g., a shape) converging to what resembles another entity but differs from it in a critically important and counter-intuitive way (in this case, having a completely different perimeter)?

If it seems that I'm having trouble articulating this question, that's because I am. But hopefully someone out there can see what I'm getting at and shed some light on the issue for me.

Answer 1

A Geometric Measure theoretic answer to your question could be the following.

Your example simply shows how things really go... There is nothing strange in it, nor in the "informal" notion of convergence you used: actually the trouble remains the same, even when all the underlying notions are well formalized.

The problem here is that the perimeter $\mathcal{P} (\cdot )$ is "only" a lower semicontinuous functional. This means: if a sequence of sets $E_n$ converges to another set $E$ in some sense (e.g. in the Hausdorff metric, which is a sort of uniform convergence for sets, or in some $L^p$ metric), then you have:

(*) $\displaystyle \mathcal{P} (E)\leq \liminf_{n\to \infty} \mathcal{P}(E_n)$;

moreover, in general the inequality is strict, even if the sequence at the RHside converges.

A less problematic example of this basic fact of GMT is the following. Let:

$E_n:=\{ (x,y)\in \mathbb{R}^2|\ x^2+y^2<1\text{ and } |y|\geq \frac{1}{n} |x|\}$,

so $E_n$ is the unit open circle with two symmetric slices (crossing the $x$ axis) removed and the slices become thinner and thinner as $n$ increases. Note that $E_n$ is a piecewise $C^1$ set with a finite number of corners, i.e. $5$, and this number does not increase with $n$ (on the contrary, in your example the number of corners becomes larger as $n\to \infty$).

Then $E_n$ converges to the unit open circle $D$ in the $L^1$ metric: in fact, the measure of the symmetric difference set $D\Delta E_n$ tends to $0$ as $n$ increases, i.e. $\lVert \chi_D -\chi_{E_n}\rVert_1\to 0$; on the other hand, one has:

$\displaystyle \mathcal{P} (E_n)=4+ 2\left( \pi -2\arctan \tfrac{1}{n}\right)$

(the summand $4$ appears because the boundary $\partial E_n$ contains four radii of lenght $=1$) therefore:

$\displaystyle \liminf_{n\to \infty} \mathcal{P}(E_n)=\lim_{n\to \infty} \mathcal{P} (E_n) =2\pi +4 >2\pi =\mathcal{P} (D)$.

For what is worth, $E_n$ converges to $D$ also in the strongest Hausdorff metric, because it is not hard to prove that the Haudorff distance:

$\displaystyle \text{dist}_H(E_n,D):=\inf \{ \epsilon >0| E_n\subseteq (1+\epsilon)D \text{ and } D\subseteq E_n+\epsilon D\}$

is given by:

$\displaystyle \text{dist}_H(E_n,D) =2-\frac{2}{\sqrt{1+\frac{1}{n^2}}}$,

and $\displaystyle \lim_{n\to \infty} \text{dist}_H(E_n,D) =0$.

If you choose $E_n$ as in your example, then you have the same situation: a sequence of sets which does converge to a triangle in some metrics (in particular, it converges in both $L^1$ and Hausdorff metric) and for which strict inequality holds in (*).

Answer 2

Not that I really know anything about it, but there's a concept called varifold, which I've seen loosely described as an "infinitesimally corrugated" manifold. I don't know how varifolds are defined rigorously, but apparently they arise in the calculus of variations when looking for surfaces of minimal area with a given boundary (like soap films on a wire loop). It might happen that a sequence of smooth surfaces converges to a would-be minimizing surface, except that the limit object is not smooth but infinitely wrinkled. This idea feels a bit like what you have here; the limit of your jagged lines should perhaps not really be considered as a normal straight line, but rather as some other kind of (infinitedly jagged) object?

Answer 3

Abstract geometry does not always match to intuitive geometry. If you are surprised from this triangle, you should be much more surprised from fractals with finite area and infinite perimeter, or fractals with a non-integer (and irrational) number as their dimension.