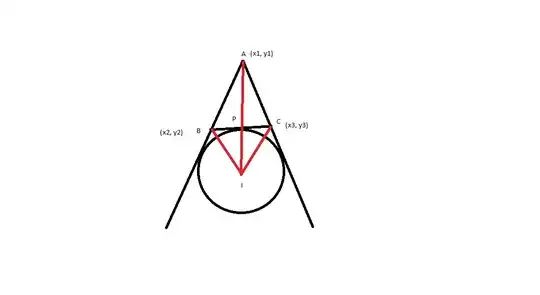
We are given the following triangle:
Here $I$ is the excenter which is formed by the intersection of internal angle bisector of $A$ and external angle bisectors of $B$ and $C$.
Consider $\triangle ABC$, $AD$ is the angle bisector of $A$, so using angle bisector theorem we get that $P$ divides side $BC$ in the ratio $|AB|:|AC|$, where $|AB|,|AC|$ are lengths of the corresponding sides.
Now using the above facts we get the point $P$ as $P(\frac{|AB|x_3+|AC|x_2}{b+c},\frac{|AB|y_3+|AC|y_2}{b+c})$.
Now, if we know the ratio in which $P$ divides $AI$ we are done, but I can't think of anything that will help me do it.
I thought of somehow proving $\triangle BIP$ and $\triangle BIA$ to be similar, to get something, but that isn't the case.
Can anyone help ?