I am just wondering that how the coordinate of the excentre comes out if we know the coordinates of vertices of the triangle.
3 Answers
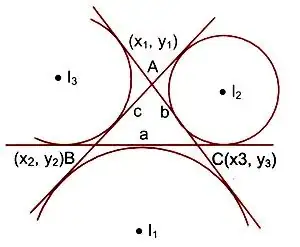
Let $A=(x_1, y_1)$, $B=(x_2, y_2)$ and $C=(x_3, y_3)$ are the vertices of a triangle $ABC,$ $c,$ $a$ and $b$ are the lengths of the sides $AB,$ $BC$ and $AC$ respectively. Then coordinates of center of ex-circle opposite to vertex $A$ are given as
$$I_1(x, y) =\left(\frac{–ax_1+bx_2+cx_3}{–a+b+c},\frac{–ay_1+by_2+cy_3}{–a+b+c}\right).$$
Similarly coordinates of centers of $I_2(x, y)$ and $I_3(x, y)$ are
$$I_2(x, y) =\left(\frac{ax_1-bx_2+cx_3}{a-b+c},\frac{ay_1-by_2+cy_3}{a-b+c}\right),$$
$$I_3(x, y) =\left(\frac{ax_1+bx_2-cx_3}{a+b-c},\frac{ay_1+by_2-cy_3}{a+b-c}\right).$$
- 90,434
-
Please try to describe as much here as possible in order to make the answer self-contained. Links are fine as support, but they can go stale and then an answer which is nothing more than a link loses its value. Please read this post. – robjohn Jan 08 '15 at 17:03
-
@robjohn OK. Edited. – Alex Ravsky Jan 10 '15 at 07:03
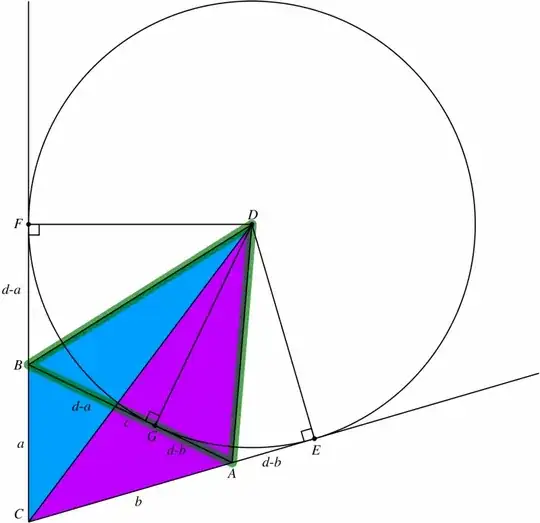
Consider the diagram:

$d=\overline{CE}=\overline{CF}$. Note that $c=\overline{AB}=(d-a)+(d-b)$. Therefore, $$ d=\frac{a+b+c}2\tag{1} $$ Furthermore, $d=\overline{CD}\cos(\theta/2)$ and $\overline{CH}=d\cos(\theta/2)$; therefore, $\overline{CH}=\overline{CD}\cos^2(\theta/2)$.
The Law of Cosines gives $$ \cos(\theta)=\frac{a^2+b^2-c^2}{2ab}\tag{2} $$ so that $$ \cos^2(\theta/2)=\frac{\vphantom{b^2}1+\cos(\theta)}2=\frac{(a+b)^2-c^2}{4ab}\tag{3} $$ $H$ is the mid-point of $\overline{EF}$; therefore, $$ \begin{align} H-C &=\frac{d}2\left(\frac{B-C}a+\frac{A-C}b\right)\\[6pt] &=\cos^2(\theta/2)(D-C)\tag{4} \end{align} $$ Putting together $(1)$, $(3)$, and $(4)$, we get $$ \begin{align} D &=C+\frac{4ab}{(a+b)^2-c^2}\frac{a+b+c}4\left(\frac{B-C}a+\frac{A-C}b\right)\\ &=C+\frac{ab}{a+b-c}\left(\frac{B-C}a+\frac{A-C}b\right)\\ &=C+\frac{a(A-C)+b(B-C)}{a+b-c}\\[6pt] &=\frac{aA+bB-cC}{a+b-c}\tag{5} \end{align} $$
- 345,667
-
1Formula $(5)$ corresponds nicely with the formula for the incenter $$\frac{aA+bB+cC}{a+b+c}$$ given in $(7)$ of this answer. – robjohn Jan 08 '15 at 22:09
-
Can you explain step (4) ? I mean how did you write $H-C$ ? Also, when you say $H$ or $C$, are you treating them as vectors ? – User9523 Aug 16 '18 at 22:26
-
1@User9523: The capital letters are points. The difference of two points is a vector; and, likewise, the sum of a point and a vector is another point. The lower case letters are distances between points. Note that $\frac{B-C}a$ and $\frac{A-C}b$ are unit vectors and so $\frac{B-C}a+\frac{A-C}b$ is in the direction of the bisector of $\angle BCA$, with length $2\cos(\theta/2)$. – robjohn Aug 17 '18 at 09:23
Consider the following diagram:
Using Barycentric Coordinates, we get that the coordinates of $D$ to be $$ D=\frac{|\triangle BCD|A+|\triangle ACD|B-|\triangle ABD|C}{|\triangle BCD|+|\triangle ACD|-|\triangle ABD|}\tag{1} $$ The weight from $\triangle ABD$ is negative since that triangle is outside of $\triangle ABC$.
Since each of the triangles in $(1)$ has the same altitude, which is the radius of the excircle, their areas are proportional to the lengths of their bases, which are the sides of $\triangle ABC$. This gives $$ D=\frac{aA+bB-cC}{a+b-c}\tag{2} $$
- 345,667