Rectangular Hyperbola - A Property of Normals

Question

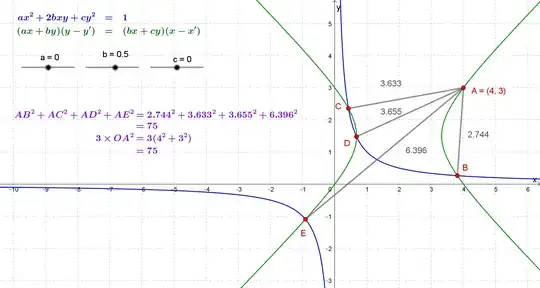
Consider the rectangular hyperbola $xy = c^2$. Normals at points $P,Q,R$ and $S$ on the curve are concurrent, and meet at point $O(h,k)$. Find $OP^2 + OQ^2 + OR^2 + OS^2$.

I managed to solve the problem using coordinate geometry, and I'm hoping to discover rather interesting methods of approaching it, here on Math SE. A solution using geometry, if possible would be great. (Of course, other methods are welcome too!)

Also, is the sum $OP^2 + OQ^2 + OR^2 + OS^2$ constant for any rectangular hyperbola, or is it something special about $xy = c^2$?

It is worth noting that a geometrical solution would probably also help us understand whether or not the result is general - addressing the second query.

Thanks a lot!

P.S. For the sake of completeness of this post, I shall share how I approached the particular result using coordinate geometry. First, I wrote the equation of the normal (in parametric form) to the given rectangular hyperbola, and plugged in $(h,k)$ into it (the coordinates of point $O$). What resulted was a fourth degree equation, and I used Vieta's theorem to directly evaluate the required expression, to get $3(h^2+k^2)$.

Answer 1

Equation of tangent at $(x_k,y_k)$,

$$y_k x+x_k y=2c^2$$

Equation of normal at $(x_k,y_k)$,

$$x_k(x-x_k)=y_k(y-y_k)$$

If $(X,Y)$ is the common point of the four normals, then

$$x_k(X-x_k)=y_k(Y-y_k)$$

Hence, all the points $(x_k,y_k)$ lie on another conic:

$$x(X-x)=y(Y-y)$$

Substitute $y=\dfrac{c^2}{x}$,

\begin{align} x(X-x) &= \frac{c^2(Yx-c^2)}{x^2} \\ x^3(X-x) &= c^2(Yx-c^2) \\ 0 &= x^4-Xx^3+c^2Yx-c^4 \end{align}

By Vieta's formulae,

\begin{align} X &= x_1+x_2+x_3+x_4 \\[5pt] 0 &= \sum_{i<j} x_i x_j \\ \sum x_k^2 &= \left( \sum x_k \right)^2-2 \sum_{i<j} x_i x_j \\ &= X^2 \\[5pt] \sum (x_k-X)^2 &= \sum (x_k^2-2x_k X+X^2) \\[5pt] &= \sum x_k^2-2X\sum x_k+4X^2 \\[5pt] &= X^2-2X^2+4X^2 \\ &= 3X^2 \end{align}

Similarly,

$$\sum (y_k-Y)^2=3Y^2$$

See also another answer here and also the case for ellipse here.

Answer 2

Proof

For convenience, we denote the coordinates of the four points $P,Q,R,S$ as $(x_i,y_i)$ where $i=1,2,3,4$, respectively.

As for $xy=c^2$, we have $$\frac{{\rm d}y}{{\rm d}x}=-\frac{c^2}{x^2}.$$ Hence, the slope of the normal at any point $(x,y)$ on the hyperbola is $$k=\frac{x^2}{c^2}.$$ Therefore, the equation of such a normal is $$\frac{y-k}{x-h}=\frac{x^2}{c^2}.$$ Put $y=\dfrac{c^2}{x}$ into it. We obtain $$x^4-hx^3+c^2kx-c^4=0,$$ apparently, which have four real roots, namely, $x_i$ where $i=1,2,3,4$, as defined above.

Thus, by Vieta's theorem, we have $$\sum x_i=h;~~~\sum_{\mathrm{cyc}}x_ix_j=0.$$Likewise, we may also have $$\sum y_i=k;~~~\sum_{\mathrm{cyc}}y_iy_j=0.$$ It follows that \begin{align*}&OP^2+OQ^2+OR^2+OS^2\\=&\sum[(x_i-h)^2+(y_i-k)^2]\\=&\sum x_i^2-2h\sum x_i+4h^2+\sum y_i^2-2k\sum y_i+4k^2\\=&\left(\sum x_i\right)^2-2\sum_{\mathrm{cyc}}x_ix_j-2h\sum x_i+4h^2+\left(\sum y_i\right)^2-2\sum_{\mathrm{cyc}}y_iy_j-2k\sum y_i+4k^2\\=&h^2-2\cdot 0-2h^2+4h^2+k^2-2 \cdot 0-2k^2+4k^2\\=&3(h^2+k^2),\end{align*}which is a constant indeed.