CONTEXT:
On the hyperbola $xy=c^2$, a possible parametrization is $P\left (cp,\frac{c}{p} \right )$. Using this, one can show with a little work that the equation of the normal is $$p^3x-py=c \left (p^4-1 \right )$$
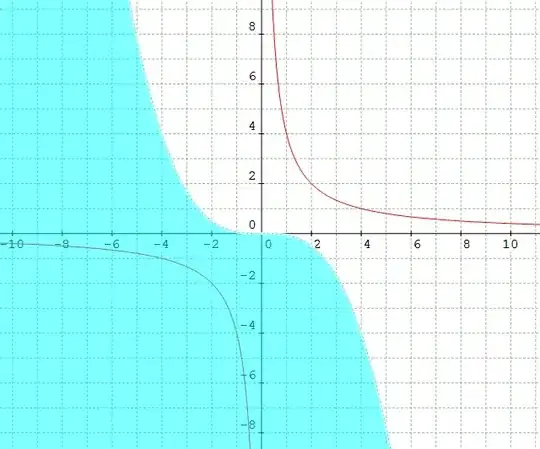
Now given that this is a quartic polynomial in $p$, it is possible for the quartic polynomial to have 4 real roots. I managed to prove that if $y>0$, then this quartic has 4 distinct real roots if $$y<-\frac{1}{4c^2}x^3$$
Geometrically, this means that from any point satisfying the above inequalities, it is possible to construct 4 distinct normals that pass through that point.
I have attached a computer generated diagram for the case when $c=2$ at the bottom of this post.
PROBLEM:
However, I cannot actually see where 4 points would be such that their normals pass through any point in the blue region, where $y>0$. I can easily see 2 points on the curve, but definitely not 4.
QUESTION:
If my work above is correct, could somebody show me where these 4 points would be, or another diagram where 4 normals intersect at the one point?