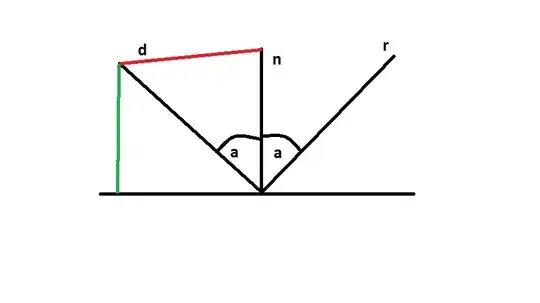
I have a raytracing exercise similar to this one here: How to get a reflection vector?.
I understand how to do the calculations but I'm having trouble visualising the projections.
The answer is $r=(d-(n\cdot d)n)+(-(n\cdot d)n)=d-2(n\cdot d)n$.
I'm thinking that $\operatorname{proj} nd=(n\cdot d)n$ = the green line and $i$ just end up at $n$.