106

I'm doing a raytracing exercise. I have a vector representing the normal of a surface at an intersection point, and a vector of the ray to the surface. How can I determine what the reflection will be?

In the below image, I have d and n. How can I get r?

Vector d is the ray; n is the normal; t is the refraction; r is the reflection

Thanks.

Nick Heiner
  • 1,231

5 Answers5

104

$$r = d - 2 (d \cdot n) n$$

where $d \cdot n$ is the dot product, and $n$ must be normalized.

Phrogz
  • 1,800
  • 2
    And if my d happens to be pointing the other direction, I need to negate it first, right? – Nick Heiner Dec 06 '10 at 18:00
  • 2
    @user2755 Yes, but you can test this yourself with pencil and paper using simple cases, e.g. $d = [1,-1]; n=[0,1]$ (incoming down and to the right onto a ground plane facing upwards). With this, $r = [1,-1] - 2 \times (-1) \times [0,1] = [1,-1] + 2 \times [0,1] = [1,-1] + [0,2] = [1,1]$. – Phrogz Dec 06 '10 at 18:06
  • 5
    I have no idea how this works, but it works, and that's all that matters. – rb3652 Jan 09 '22 at 18:53
  • 2
    @rb3652 Here is my understanding. $d\cdot n$ is the length of $d$ along the direction of $n$ (i.e., the "projection" of $d$ onto $n$). Multiplying by $n$ turns this scalar $d\cdot n$ into a vector of length $d$ along the direction $n$. If you substracted this from $d$, you would remove all of the $n$-direction character from $d$ (i.e., it would be perpendicular to $n$ and would be parallel to b in the diagram). Subtracting it again yields a vector that is reflected back since you're effectively adding the $n$-direction character in the opposite direction of $d$ again. – tarheels Jul 18 '23 at 13:20
89

Let $\hat{n} = {n \over \|n\|}$. Then $\hat{n}$ is the vector of magnitude one in the same direction as $n$. The projection of $d$ in the $n$ direction is given by $\mathrm{proj}_{n}d = (d \cdot \hat{n})\hat{n}$, and the projection of $d$ in the orthogonal direction is therefore given by $d - (d \cdot \hat{n})\hat{n}$. Thus we have $$d = (d \cdot \hat{n})\hat{n} + [d - (d \cdot \hat{n})\hat{n}]$$ Note that $r$ has $-1$ times the projection onto $n$ that $d$ has onto $n$, while the orthogonal projection of $r$ onto $n$ is equal to the orthogonal projection of $d$ onto $n$, therefore $$r = -(d \cdot \hat{n})\hat{n} + [d - (d \cdot \hat{n})\hat{n}]$$ Alternatively you may look at it as that $-r$ has the same projection onto $n$ that $d$ has onto $n$, with its orthogonal projection given by $-1$ times that of $d$. $$-r = (d \cdot \hat{n})\hat{n} - [d - (d \cdot \hat{n})\hat{n}]$$ The later equation is exactly $$r = -(d \cdot \hat{n})\hat{n} + [d - (d \cdot \hat{n})\hat{n}]$$

Hence one can get $r$ from $d$ via $$r = d - 2(d \cdot \hat{n})\hat{n}$$ Stated in terms of $n$ itself, this becomes $$r = d - {2 d \cdot n\over \|n\|^2}n$$

Community
  • 1
Zarrax
  • 44,950
8

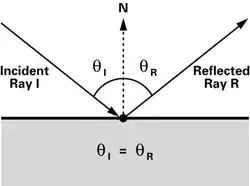
I was trying to understand how to calculate the reflection vector and found these answers. I couldn't understand them easily, so I took my time to do it myself, the good thing is that I can now detail it in an ELI5 fashion!

I did develop the formula using the 3 steps shown in the graphic. I describe them bellow.

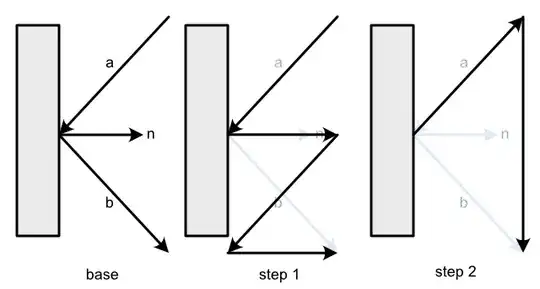
Steps to compute the rfection vector

So, the initial situation is $\vec{a}$ pointing toward a plane. Then we have the normal $\vec{n}$ of unit lenght and we would like to find $\vec{b}$

So, the first step is using the dot product to get a vertical vector that will be used in step 2.

With step 1 my partial formula is: $2\times\left(a+(-\vec{a})\cdot\vec{n}\times{}n\right)$

mind the change of sign of $\vec{a}$ above, we "flipped" it

Then in step 2, I can write: $-\vec{a}+2\times\left(a+(-\vec{a})\cdot\vec{n}\times{}n\right)$

Now, I can distribute: $-\vec{a}+2\times{}\vec{a}+2\times(-\vec{a})\cdot\vec{n}\times{}n$

Then simplify, and I end up with: $\vec{a}+2\times(-\vec{a})\cdot\vec{n}\times{}n$

If you negate a vector in the dot product, you negate the result of the dot product.

$\vec{a}\cdot\vec{b}=-(-\vec{a})\cdot\vec{b}$

That means that I can rewrite the formula like this:

$\vec{a}-2\times(\vec{a})\cdot\vec{n}\times{}n$

programaths
  • 181
  • 1
    Thank you. Though the way you used Cross Product's notation as a multiplication notation confused me big time. – Orange Cat Sep 13 '22 at 05:30
1

Suppose that $d$ and $r$ have the same magnitude. $$ \lVert r \rVert = \lVert d \rVert $$ From the reflection relationship, we have this equality about cross products. $$ r \times n \ = \ d \times n \\ \therefore \ \left( r \ - d \right) \times n \ = \ \vec{0} $$ which means $$ r \ - d \ = s \ n \\ \therefore \ r \ = \ d \ + s \ n $$ where $s$ is a real number.
Taking their squares, we have $$ \lVert r \rVert ^2 \ = \ \lVert d \rVert ^2 + \ 2\ s \left( d \cdot n \right) \ + s^2 \ \lVert n \rVert ^2 \\ \therefore \ s \left( s \ \lVert n \rVert ^2 + \ 2 \ (d \cdot n) \right) = 0 \\ $$ So $$ s \ = 0 \ , - \frac{2 \ (d \cdot n)}{\lVert n \rVert ^2} $$ Since $s = 0 \ $ means $ \ d \ $ itself, we take the other value and get $$ r \ = \ d - \frac{2 \ (d \cdot n)}{\lVert n \rVert ^2} \ n $$

Dugnutt
  • 11
0

In case you want to rotate about Y axis you can use the following instead. This is mostly useful for computer graphics applications. Note that $d$ is assumed to be pointing outward in the equation below (i.e. ignore the direction of $d$ in the picture below) and $n$ needs to be normalized:

enter image description here

$$r = 2 (d \cdot n) n - d$$

Amir
  • 435