On The Parametric Equation Of A Parabola

Question

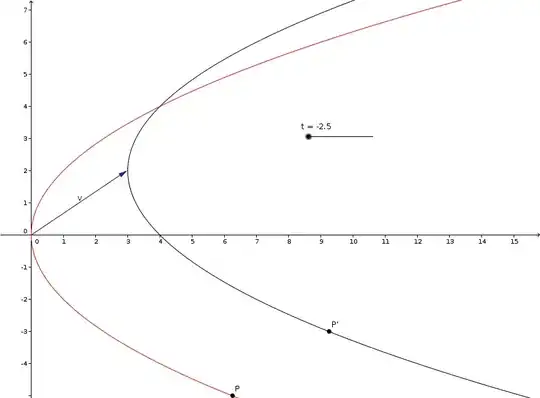
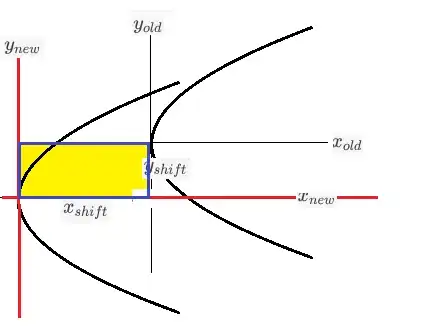
Let's look at a parabola with an equation $(y-k)^2=4a(x-h)$. I'm struggling to understand why its parametric equation would be $x=h+at^2$ and $y=k+2at$. Since it is being subtracted by $h$ and $k$ respectively, why would its $x$ and $y$ values increase/have $h$ and $k$ added to them instead?

I understand that since each $x$-value is being subtracted by $h$, each $x$-value needs to be $h$ bigger to "achieve" the same y-value. But that also means that for each $y$-value, each $x$-value will be h smaller right? So how does subtracting by $h$ increase the value of $x$ by $h$, as shown in the parametric equation $x=h+at^2$? I ask the same question for $y=k+2at$.

Anyways, I have no idea what the "x" output the parametric equation gives out even means? Does the parametric equation give out the x-value which will be inputted into the equation? But then no matter where the graph is, that doesn't change what x-value would be inputted into the equation, right? So why would subtracting x by h change the parametric equation of x either, if x will remain unchanged?

Or does the parametric equation give out the x-value as in the x-value to be plotted on the graph? But then if so, I still don't get why the sign would be +h, instead of -h. Yes, in the graph, for every y-value, the x-value of a graph y^2=4a(xx-h) would be left of the original graph. But how do we know the parametric equation refers to the x-value for every given y-value. And if that is not what is referred to by the parametric equation, why are we subtracting?

Can someone explain this to me as simply as possible, since I'm still a beginner. I'm just putting this as a precaution, and try not to use Calculus in the response, since I haven't learnt it yet.

Answer 1

Let's start with the simplest case, in which $h$ and $k$ are both $0$. Then the parabola is $$y^2 = 4ax$$ and the parametric equation is $$y=2at, \hskip{0.5in} x=at^2$$ and you can directly verify that $$y^2 = (2at)^2 = 4a^2t^2 = 4a(at^2) = 4ax$$ so everything works nicely.

Now let's consider the general case. We have $$(y-k)^2 = 4a(x-h)$$ If we introduce (temporarily) the new variables $u = x-h, v = y-k$ then the equation can be written as $$v^2 = 4au$$ which has exactly the form of the simple case we already considered. So we know the parametric equations for $u$ and $v$ are $$v=2at, \hskip{0.5in} u=at^2$$ But now we remember that $u = x-h$ and $v = y-k$. That means the parametric solutions are $$y-k=2at,\hskip{0.5in} x-h=at^2$$ which leads directly to the solution $$y=k+2at,\hskip{0.5in} x=h+at^2$$

Now let's look back and try to understand what's happening. The main idea is that the "shift" induced by replacing $x$ and $y$ with $x-h$ and $y-k$, respectively, corresponds to a shift in the solution that also replaces $x$ and $y$ with $x-h$ and $y-k$. The "plus" sign just comes from moving the negative terms to the other side of the equals sign.

Answer 2

Note that a parametric representation of $$Y^2=4aX$$ is $X=at^2$ and $Y=2at$. What happens when $X=x-h$ and $Y=y-k$?

Answer 3

Explaining parametrization

Let's start with the simpler case $Y^2=4aX$, which, in the $XY$-plane, is a parabola with horizontal axis of symmetry and vertex in the origin. A parametric representation is \begin{cases} X=at^2\\ Y=2at \end{cases}

While it's clear that $X$ and $Y$ values are the coordinates in the $XY$-plane, what is the parameter $t$? For every value of $t\in\mathbb{R}$ parametric equations yield a point $P(t)=(at^2,2at)$ on the parabola. Imagine $t$ indicates the time, then $P(t)$ is the position on the parabola at the moment. In our case:

• when $t=0$, $P$ is on the vertex
• when $t>0$, $P$ is on the upper branch
• when $t<0$, $P$ is on the lower branch

See the red parabola in the gif below.

Applying a translation

Now consider the following translation $$ \begin{cases} x=X+h\\ y=Y+k \end{cases} \quad\equiv\quad \begin{cases} X=x-h\\ Y=y-k \end{cases} $$ Applying this transformation to our case (aka substitution) gives the parabola $$(y-k)^2=4a(x-h)^2$$ and the respective parametric representation $$ \begin{cases} x-h=at^2\\ y-k=2at \end{cases} \implies \begin{cases} x=h+at^2\\ y=k+2at \end{cases} $$

These equations, in the $xy$-plane, represent a parabola identical to the previous one, only shifted by a vector $\mathbf{v}=(h,k)$. Moreover every value $t$ yields a point $P'(t)=(h+at^2,k+2at)$ on the second parabola. Notice that $$ P'(t)=P(t)+\mathbf{v}\qquad\forall t\in\mathbb{R}$$

Addressing your doubts

The values of $x$ and $y$ are the coordinates in the $xy$-plane. Whether you put them into the parabola equation or obtain them from the parametric equations, $(x,y)$ are coordinates.

The parabola equation gives you a direct relation between $x$ and $y$. Each and every point of the parabola must satisfy this relation (a curve is the locus defined by its equation).

On the other hand, parametric equations represent each point of the parabola as a function of the parameter $t$. Think of $t$ as the time, then $P(t)$ is your trajectory on the plane. Of course changing parametric equations will change the starting point and the velocity of your trajectory, but the path will be the same.

When you apply a translation by a vector $\mathbf{v}=(h,k)$, everything get shifted by $h$ in the $x$-direction and by $k$ in the $y$-direction. That's why $P'=(x_{P'},y_{P'})=(x_P+h,y_P+k)=P+\mathbf{v}$.

Wait! What about the curve equation? Why do you get '$x-h$' and '$y-k$'? Remember that the parabola equation describes a relation between certain points. In order to exploit that relation you need to bring back those points in their original position (actually, when you go and substitute, maths does that for you).

Consider the equation $x^2+y^2=0$ which is satisfied only by $(0,0)$, the origin of the $xy$-plane. Apply the following translation \begin{cases} x'=x+1\\ y'=y+2 \end{cases} What is the point of the $x'y'$-plane that correspond with the origin? Of course it is $(1,2)$. And which equation does it satisfy? $(x'-1)^2+(y'-2)^2=0$.

A visual aid

The gif here below represents the $XY$-plane and the $xy$-plane overlapping each other. You can see the original parabola (red), the shifted one (black), and the points $P(t)$ and $P'(t)$ (for this example I set $a=1$, $h=3$, $k=2$).

Answer 4

Let the parametrization $ (f(t),g(t))$ be anything, it doesn't matter... it is just a simple translation parallel to axes, meaning addition or subtraction of $(x,y)$ coordinates of any curve in order to get to the new pair from the old pair.

In this case it is a particular case of a parabola with $x$ axis of symmetry, $t=0$ corresponding to the vertex of parabola described by old pair.

$$ x_{new}= x_{shift} + f(t);\quad y_{new} =y_{shift}+ g(t); $$ $$ x_{new}= x_{shift} + x_{old}\,;\quad y_{new} =y_{shift}+ y_{old}\,;$$

Dynamically it is motion of a particle starting from origin when gravity acts along old $x-$ axis:

$$ \,x= a t^ 2, y= 2 a t,\,$$

where $t$ is not time but reciprocal of varying slope of the parabola of focal length $a$.

The very same motion is given by new axes with new parametrization if you reckon with new shifted datum. In the new case the old trajectory of course just does not exist.

Answer 5

Let us try $$(y-k)^2=4a(x-h)=4a^2t^2,$$ then $$y=k\color{red}\pm 2at,\quad x=h+at^2.\tag1$$ Formulas $(1)$ take in account that the parabola has two branches.

Therefore, the issue parametric function presents only one branch of parabola.