-1

This is to finish Hw to find the two second order linear recursive common items?

Here is a recent question, very similar, the only response also used pari Thue: Integer solutions to diophantine equation $x^4+4x^3y-6x^2y^2-4xy^3+y^4=1$

Can anyone confirm that the only integer solutions to

$$ r^4 - 8 r^3 s + 2 r^2 s^2 + 8 r s^3 + s^4 = 1 $$ really are $$ (1,0) \; ; \; (-1,0) \; ; \; (0,1) \; ; \; (0,-1) \; \; ? $$ This could easily be equivalent to some published result of similar type. For a time I had Mordell's book on Diophantine equations, he settled some of these. Notice that if both $r,s$ are 1, we get 4 rather than one. Put another way, $r+s$ must be odd. This is also linked with Pythagorean triples, that is how I got it, actually.

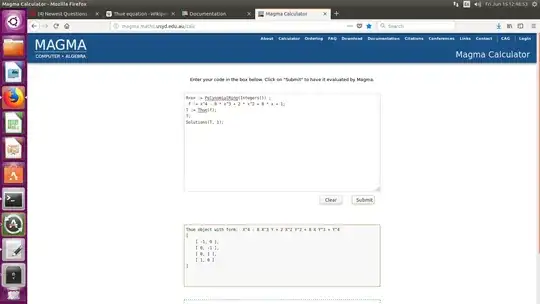
I think i did this correctly, gp-Pari on my home machine, including flag for ignoring GRH (I was attempting to get an unconditional result):

? tnf = thueinit(  t^4 - 8*t^3 + 2*t^2 + 8*t + 1 , {1}) ;  
? thue(tnf,1)
%10 = [[0, 1], [0, -1], [1, 0], [-1, 0]]

Full text of init:

?  tnf = thueinit(  t^4 - 8*t^3 + 2*t^2 + 8*t + 1 , {1})
%9 = [[x^4 - 8*x^3 + 2*x^2 + 8*x + 1, 1, 1], [[;], matrix(0,6), [0.6584789484624083543125231737 + 18.84955592153875943077586030*I, 0.8813735870195430252326093250 + 9.424777960769379715387930150*I, -1.146215834780588843900393656 - 9.424777960769379715387930150*I; -0.6584789484624083543125231737 + 12.56637061435917295385057353*I, -0.8813735870195430252326093250 + 6.283185307179586476925286767*I, -1.146215834780588843900393656 - 6.283185307179586476925286767*I; 0.6584789484624083543125231737 + 9.424777960769379715387930150*I, -0.8813735870195430252326093250 + 6.283185307179586476925286767*I, 1.146215834780588843900393656 - 3.141592653589793238462643383*I; -0.6584789484624083543125231737 + 9.424777960769379715387930150*I, 0.8813735870195430252326093250 + 3.141592653589793238462643383*I, 1.146215834780588843900393656 - 1.175494351 E-38*I], [0.3946857140156758737830649825 + 3.141592653589793238462643383*I, 0.1959185839666155345215995043, -0.6473652729907846885320837159 + 3.141592653589793238462643383*I, -0.2438684431590902447939352410 + 3.141592653589793238462643383*I, -5.87747175 E-39 + 3.141592653589793238462643383*I, 0.5444978613266737698152897111 + 3.141592653589793238462643383*I; -0.6017179734539150740851039446 + 3.141592653589793238462643383*I, 0.01111367547162366578043945774 + 3.141592653589793238462643383*I, 0.8543975324290238888341226780, -0.9023473916214985991064584147, -8.81620763 E-39, 1.540901548796264717683458638; 0.01111367547162366578043945774 + 3.141592653589793238462643383*I, -0.6017179734539150740851039446 + 3.141592653589793238462643383*I, -0.2637932344467324805294581912, 0.9023473916214985991064584147, -8.81620763 E-39 + 3.141592653589793238462643383*I, -0.9502972508139733093787941514; 0.1959185839666155345215995043, 0.3946857140156758737830649825 + 3.141592653589793238462643383*I, 0.05676097500849328022741922908, 0.2438684431590902447939352410, 3.232609465 E-38, -1.135102159308965178119954198], [[23, [-9, 0, -2, 1]~, 1, 1, [-3, -14, -22, 21; -2, -17, -7, 14; -10, 7, 11, -22; 7, 2, -10, -3]], [23, [-1, 0, -2, 1]~, 1, 1, [1, -15, 3, 30; -11, -19, -10, 15; 7, 10, 21, 3; 10, 11, 7, 1]], [23, [0, 0, -2, 1]~, 1, 1, [11, 10, -4, 15; 8, 1, -5, -10; -6, 5, 21, -4; 5, -8, -6, 11]], [2, [1, -1, 0, 0]~, 4, 1, [1, 3, 3, 3; 1, -1, -1, -3; 1, 1, 3, 3; 1, -1, 1, 1]], [3, [12, 4, -14, 7]~, 2, 2, [0, 3, 3, 3; 1, -2, -1, -3; 1, 1, 2, 3; 1, -1, 1, 0]], [23, [10, 0, -2, 1]~, 1, 1, [-5, -29, -31, -12; -9, 3, 4, 29; -11, -4, -13, -31; -4, 9, -11, -5]]], 0, [x^4 - 8*x^3 + 2*x^2 + 8*x + 1, [4, 0], 2304, 16, [[1, 1.931851652578136573499486400, 0.5176380902050415246977976753, -1.732050807568877293527446342; 1, 0.5176380902050415246977976753, 1.931851652578136573499486400, 1.732050807568877293527446342; 1, -1.931851652578136573499486400, -0.5176380902050415246977976753, -1.732050807568877293527446342; 1, -0.5176380902050415246977976753, -1.931851652578136573499486400, 1.732050807568877293527446342], [1, 1.931851652578136573499486400, 0.5176380902050415246977976753, -1.732050807568877293527446342; 1, 0.5176380902050415246977976753, 1.931851652578136573499486400, 1.732050807568877293527446342; 1, -1.931851652578136573499486400, -0.5176380902050415246977976753, -1.732050807568877293527446342; 1, -0.5176380902050415246977976753, -1.931851652578136573499486400, 1.732050807568877293527446342], [1, 2, 1, -2; 1, 1, 2, 2; 1, -2, -1, -2; 1, -1, -2, 2], [4, 0, 0, 0; 0, 8, 4, 0; 0, 4, 8, 0; 0, 0, 0, 12], [12, 0, 0, 0; 0, 12, 4, 0; 0, 0, 4, 0; 0, 0, 0, 4], [3, 0, 0, 0; 0, 2, -1, 0; 0, -1, 2, 0; 0, 0, 0, 1], [3, [0, 3, 3, 0; 1, 0, 0, -3; 1, 0, 0, 3; 0, -1, 1, 0]], [2, 3]], [-0.7673269879789603429230416920, -0.1316524975873958534715264574, 1.303225372841205755868149009, 7.595754112725150440526419140], [1, 1/4*x^2 - 2*x + 1/4, 1/4*x^3 - 2*x^2 + 1/4*x + 2, 1/2*x^3 - 4*x^2 + 3/2*x + 2], [1, 2, 15, 110; 0, 0, 4, 32; 0, -2, -16, -122; 0, 1, 8, 63], [1, 0, 0, 0, 0, 2, 1, 0, 0, 1, 2, 0, 0, 0, 0, 3; 0, 1, 0, 0, 1, 0, 0, -2, 0, 0, 0, -1, 0, -2, -1, 0; 0, 0, 1, 0, 0, 0, 0, 1, 1, 0, 0, 2, 0, 1, 2, 0; 0, 0, 0, 1, 0, -1, 0, 0, 0, 0, 1, 0, 1, 0, 0, 0]], [[1, [], []], 2.660898580190370468920683696, 1, [2, -1], [1/4*x^2 - 2*x + 1/4, 1/4*x^3 - 9/4*x^2 + 9/4*x + 3/4, 1/4*x^3 - 7/4*x^2 - 3/4*x + 1/4]], [[;], [], []], [0, []]], [-0.7673269879789603429230416920, -0.1316524975873958534715264574, 1.303225372841205755868149009, 7.595754112725150440526419140]~, [0.6584789484624083543125231737, 0.8813735870195430252326093250, 1.146215834780588843900393656]~, [1.931851652578136573499486400, -2.414213562373095048801688724, -0.3178372451957822447257576173; 0.5176380902050415246977976753, 0.4142135623730950488016887242, 0.3178372451957822447257576173; -1.931851652578136573499486400, 0.4142135623730950488016887242, -3.146264369941972342329135066; -0.5176380902050415246977976753, -2.414213562373095048801688724, 3.146264369941972342329135066], [0.7593257175002069232189841229, 3.053650672 E-87, 0.7593257175002069232189841229; 0.E-86, -0.5672963285532554920286227026, -0.5672963285532554920286227026; -0.4362180183069195686937970696, -0.4362180183069195686937970696, 0], [1.1350278051283338153, 0.6356744904551319385, 0.5731079173902944219501968278, 1.0000000000000000000, 5.17610227 E-85, 11, 1]]
? thue(tnf,1)
%10 = [[0, 1], [0, -1], [1, 0], [-1, 0]]
?
Will Jagy
  • 139,541

1 Answers1

0

Magma have changed their command names, very recently I suspect

enter image description here

Let me paste in as text also:

http://magma.maths.usyd.edu.au/calc
(input):
R<x> := PolynomialRing(Integers()) ;
 f := x^4 - 8 * x^3 + 2 * x^2 + 8 * x + 1;
T := Thue(f);
T;
Solutions(T, 1);

(output):
Thue object with form:  X^4 - 8 X^3 Y + 2 X^2 Y^2 + 8 X Y^3 + Y^4
[
    [ -1, 0 ],
    [ 0, -1 ],
    [ 0, 1 ],
    [ 1, 0 ]
]
Will Jagy
  • 139,541