Given two sequences
$$a(n)=4a(n-1)-a(n-2), \quad a(1)=1，\; a(2)=5;$$ $$b(n)=10b(n-1)-b(n-2), \quad b(1)=1，\; b(2)=11.$$
If some $a(n)=b(m)$, $m,n\in\mathbb{N}$, exist?(Except a(1)=b(1) ) If there are no common items, how to prove it?
The Two solution equation follows from wolfram alpha.
Thanks a lot, I love you master!
Linear difference equations are much like differential equations
To solve
$$ a_n = 4 a_{n-1}-a_{n-2},\: a_1=1,\; a_2 = 5 $$
we assume that $a_n = \alpha^n$ and substituting results in
$$ (1-4\alpha+\alpha^2)\alpha^n = 0 $$
now solving
$$ 1-4\alpha+\alpha^2 = 0 $$
gives
$$ a_n = c_1(-2-\sqrt5)^n+c_1(-2+\sqrt5)^n $$
Analogously for
$$ b_n = c_3(5-2\sqrt6)^2+c_4(5+\sqrt6)^n $$
Considering the initial conditions we have
$$ a_n =-\frac{\left(1+\sqrt{3}\right) \left(2 \left(2-\sqrt{3}\right)^n+\sqrt{3} \left(2-\sqrt{3}\right)^n-\left(2+\sqrt{3}\right)^n\right)}{2 \left(2+\sqrt{3}\right)} = \frac{1}{2} \left(1+\sqrt{3}\right) \left(\left(2+\sqrt{3}\right)^{n-1}-\left(2-\sqrt{3}\right)^n\right) $$
and
$$ b_n = -\frac{\left(2+\sqrt{6}\right) \left(5 \left(5-2 \sqrt{6}\right)^n+2 \sqrt{6} \left(5-2 \sqrt{6}\right)^n-\left(5+2 \sqrt{6}\right)^n\right)}{4 \left(5+2 \sqrt{6}\right)} = \frac{1}{4} \left(2+\sqrt{6}\right) \left(\left(5+2 \sqrt{6}\right)^{n-1}-\left(5-2 \sqrt{6}\right)^n\right) $$
I hope this helps.
NOTE
$$ a_n = \eta_n + \gamma_n\sqrt 3\\ b_n =\xi_n+\mu_n\sqrt6 $$
I do not think this is elementary. For your sequence called $a_n \; ,$ you are giving the $x$ values in the Pell type $$ x^2 - 3 y^2 = -2. $$ For your sequence called $b_n \; ,$ you are giving the $x$ values in the Pell type $$ 2x^2 - 3 z^2 = -1. $$ Multiply and subtract, whenever there is a common $x$ value, $$ z^2 - 2 y^2 = -1. $$
There are results, for example in Mordell's book, on pairs of Pell type equations. I will see if I can find anything. This question has some references (but no final resolution) A System of Simultaneous Pell Equations
Alright, SZALAY gives an algorithm for completely solving this sort of thing.
I did not realize that this problem moves naturally into my area, ternary quadratic forms. The outcome is that the overlap you have already found is the only one. I found out this simple technique from reading Szalay. Oh, it all reduces to confirming that there are only trivial integer solutions to a quartic, I put the information and a request for confirmation at Quartic: using a Thue tool truly
Alright, we have $$ x^2 - 3 y^2 = -2$$ and $$ 2x^2 - 3 z^2 = -1$$ Multiply these by $-1$ and $2$ to get $$ -x^2 + 3 y^2 = 2 \; , $$ $$ 4 x^2 - 6 z^2 = -2 \; , $$ so $$ 3x^2 + 3 y^2 - 6 z^2 = 0 \; , $$ finally $$ x^2 + y^2 = 2 z^2. $$ Since we can see from the original Pell type equations that $z$ must be odd, meanwhile $\gcd(x,y,z) = 1.$
Here is the part related to Pythagorean triples, but adjusted for $x^2 + y^2 = 2 z^2$: all (primitive) triples can be formed by $$ x = r^2 + 2rs - s^2 \; , $$ $$ y = r^2 - 2rs - s^2 \; , $$ $$ z = r^2 + s^2. $$ Actually, for any of the three variables you can choose $\pm \; .$ See Parametric characterization for $x^2 + y^2 = 2z^2$
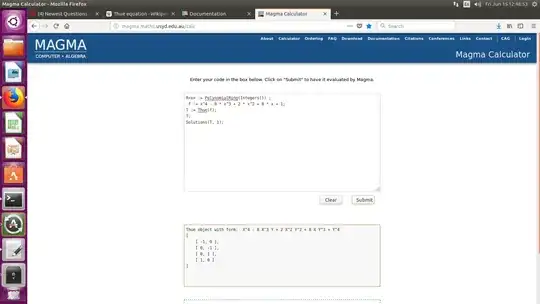
Plugging back in, either to $x^2 - 3 y^2 = -2$ or $2 x^2 - 3 z^2 = -1,$ we get the (integer) equation $$ r^4 - 8 r^3 s + 2 r^2 s^2 + 8 r s^3 + s^4 = 1. $$ This is called a Thue equation. I ran it in gp-Pari, the only solutions are $$ (1,0) \; ; \; (-1,0) \; ; \; (0,1) \; ; \; (0,-1) $$ so that the $x,y,z$ triples can only be made up of $\pm 1 \; .$
I also ran it in the online MAGMA calculator. The syntax in June 2018 has updated compared with published articles.
