How to find the derivative of the sine from the definition of derivative?

Question

How to find the derivative of this function: $f(x) = \sin(x)$ - using definition of derivative:

\begin{equation} f'(x) = \lim_{h\to0}\dfrac{f(x + h) - f(x)}{h} \end{equation}

Answer 1

Here is a "proof without words" that $\displaystyle\frac{\mathrm{d}\sin(\theta)}{\mathrm{d}\theta}=\cos(\theta)$

$\hspace{7mm}$

Answer 2

Using the addition formula we have: $$ \frac{f(x+h)-f(x)}{h}=\frac{\sin(x+h)-\sin(x)}{h}=\frac{\sin(x)\cos(h)+\sin(h)\cos(x)-\sin(x)}{h}\\ =\sin(x)\frac{\cos(h)-1}{h}+\cos(x)\frac{\sin(h)}{h}. $$ Now let $h\to 0$ and apply that $\lim_{h\to 0}\frac{\sin (h)}{h}=1$ and $\lim_{h\to 0}\frac{\cos(h)-1}{h}=0$ (these can be found e.g. here).

Answer 3

Applying $\sin C-\sin D=2\sin\left(\frac{C-D}2\right)\cos\left(\frac{C+D}2\right),$

If $f(x)=\sin(mx+E)$ where $m,E$ are arbitrary constants and $m\ne0$

So, $$f(x+h)-f(x)=\sin\{m(x+h)+E\}-\sin(mx+E)$$ $$=2\sin\left(\frac{(mx+mh+E)-(mx+E)}2\right)\cos\left(\frac{(mx+mh+E)+(mx+E)}2\right)$$ $$=2\sin\left(\frac{mh}2\right)\cos\left(mx+E+\frac{mh}2\right)$$

$$f'(x)=\lim_{h\to 0}\frac{f(x+h)-f(x)}h$$ $$=m\lim_{\frac{mh}2}\frac{\sin\left(\frac{mh}2\right)}{\frac{mh}2}\lim_{\frac{mh}2\to 0}\cos\left(mx+E+\frac{mh}2\right)$$ as $\frac {mh}2\to 0$ as $h\to 0$

Hence, $$\frac{d\sin(mx+E)}{dx}=m\cos(mx+E)$$

Here $m=1,E=0$

Answer 4

here's an alternative (geometric) proof of the formula [sin(x)]'=cos(x): http://www.maa.org/pubs/Calc_articles/ma006.pdf .

Answer 5

[I love the proof without words from @robjohn, but I have had attentive students object that the triangle is not a real triangle since it is an arc of a circle and that the true hypotenuse does not equal the arc length $d\theta$. Here is a more rigorous way to satisfy such objections to this important way of looking at the derivatives of sine and cosine.]

Let $\theta$ be an angle, say, in the first quadrant, and let $\Delta\theta$ represent a small change in the angle. Let $P$, $Q$ be the points with coordinates $$P=(\cos \theta,\sin \theta) \quad{\rm and}\quad Q=(\cos (\theta+\Delta\theta),\sin (\theta+\Delta\theta))\,.$$ Let $\Delta s$ be the length of $PQ$, $\Delta x$ be the change in $x$ from $P$ to $Q$, and $\Delta y$ be the change in $y$. (In other words, $\Delta x =\cos(\theta+\Delta\theta)- \cos \theta$ and $\Delta y= \sin(\theta+\Delta\theta) -\sin \theta$.) Next construct a triangle, similar to the small right triangle in the figure below with $PQ$ as the hypotenuse, whose sides have lengths equal to the corresponding sides of the small triangle divided by $\Delta\theta$. (See figure.)

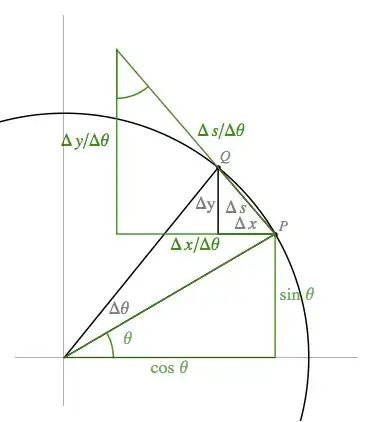
Now let $\Delta\theta \rightarrow 0$. The secant through $PQ$ will approach the tangent through $P$; we also get the following limits:

$$\lim_{\Delta\theta\rightarrow 0}{\Delta s \over \Delta\theta}=1,\quad \lim_{\Delta\theta\rightarrow 0} {\Delta x \over \Delta\theta} ={dx\over d\theta},\quad\hbox{and}\quad \lim_{\Delta\theta\rightarrow 0} {\Delta y \over \Delta\theta}={dy \over d \theta}\,.$$

(The first is because $\Delta s = {1\over2}\sin {1\over2}\theta$ and the limit follows from $\lim_{u\rightarrow0} (\sin u)/u = 1$.) In the limiting figure below, the two right triangles become congruent since the hypotenuses are 1 unit and the marked angles each equal $\theta$. Therefore the corresponding sides have the same magnitude. Hence $${dy \over d \theta}=\cos \theta\quad\hbox{and}\quad{dx \over d \theta}=-\sin \theta\,.$$ Since $y=\sin \theta$ and $x = \cos \theta$, this shows what was to be shown.