14

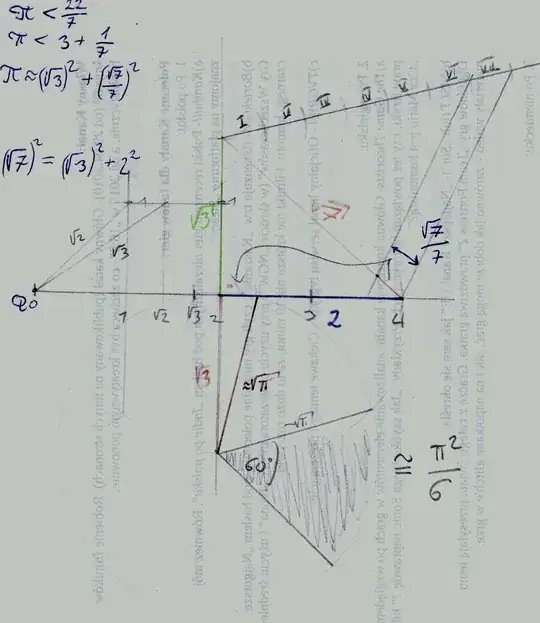
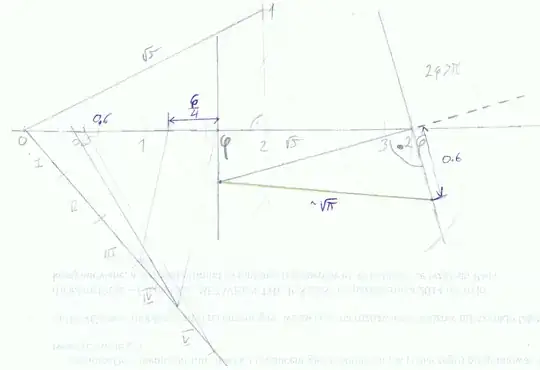
There are several proofs to the solution of the well-known Basel Problem, i.e. $$\sum_{n=1}^\infty \frac 1{n^2}=\frac {\pi^2}6$$

Is is possible to create a geometrical interpretation of this identity in the form of the area of $\frac 16$ of a circle with radius $\sqrt{\pi}$?

Hypergeometricx
  • 22,657
  • 8
    I havent actually watched this yet, but 3blue1brown usually has great geometric insights https://www.youtube.com/watch?v=d-o3eB9sfls – pancini Jun 03 '18 at 17:13
  • 1
    Suppose there were such an interpretation. Then the right hand side has units of area, which means that the terms on the left side do as well. But then each of the $n$s on the left need to represent something of units of reciprocal length, which may be difficult/unnatural. (I'm not saying it's impossible, but this is an issue you;d have to deal with.) – Mark S. Jun 03 '18 at 17:17
  • 1
    @ElliotG The 3Blue1Brown video has great insights but it does not take the area as OP has thought of here. Still it is a good video I'd recommend for understanding the Basel problem – The Integrator Jun 03 '18 at 17:18
  • 4
    It is more likely to have a geometric interpretation of $\zeta(2)$ as the volume of a torus. By creative telescoping it is simple to prove that $\zeta(2)$ is related to $\arcsin^2\left(\frac{1}{2}\right)$. – Jack D'Aurizio Jun 03 '18 at 17:30
  • Units is not really a big issue. A bigger issue is that the radius is a trancendental number. Fitting simple shapes of area $6/n^2$ (a rational number) inside such a circle seems highly non-trivial. – Winther Jun 03 '18 at 18:07
  • 1
    You mean radius $\pi$, right? If the radius is $\sqrt{\pi}$, then the area is $\pi/6$... – Hans Lundmark Jun 03 '18 at 20:31
  • 2
    @HansLundmark if the radius is $\sqrt \pi$ then area $A = \dfrac16 \pi r^2= \dfrac16 \pi \pi = \dfrac{\pi^2}6$ – The Integrator Jun 04 '18 at 07:23
  • No. You are taking the radius to the fourth power. The square of the square root of $\pi$ is $\pi$. – Hans Lundmark Jun 04 '18 at 07:27
  • 2
    @HansLundmark exactly $r^2 = (\sqrt\pi)^2 =\pi $ together with the other $\pi$ it becomes $\pi^2$ – The Integrator Jun 04 '18 at 07:31
  • Ah, sorry... Stupid me. – Hans Lundmark Jun 04 '18 at 07:43
  • @HansLundmark its alright , ive made stupider mistakes – The Integrator Jun 04 '18 at 07:48
  • Very interesting, @JackD'Aurizio. For a torus, $\pi^2$ appears naturally, so no need for transcendental dimensions. Can you develop the idea further? – Hypergeometricx Jun 04 '18 at 16:47
  • Thanks, everyone, for your comments. – Hypergeometricx Jun 04 '18 at 16:47
  • @hypergeometric: have a look at https://math.stackexchange.com/a/1931109/44121 – Jack D'Aurizio Jun 04 '18 at 17:05

3 Answers3

0

(For the best expierience- please use a compass)

I. An approximation for $\sqrt{\pi}$ : enter image description here II. How to split a circle into 6 equal part: enter image description here

EDIT: Epilog and history:

I have start w/ some famous square roots (without a compass): enter image description here On this way we can win by hand roots like $\sqrt{3}$; $\sqrt{10}$ since $=\sqrt{ 3^2+1^2}$

Note: $\sqrt{3}<\sqrt{\pi}$ and $\pi<\sqrt{10}$

or the golden ratio- we need add to $1$ with the compass the $\sqrt{5}$ (or vice versa) and split in the middle: enter image description here

Krzysztof Myśliwiec
  • 201
0

TOPIC: Area of $\frac{1}{6}$ of Circle with Radius $\sqrt{\pi}$

Last time I show how to get an easy approximation for radius via Pythagorean theorem: $$ (\sqrt{\pi})^2\geq1.7^2+0.5^2 $$ and have give a suggestion to do different- let me show for $\pi\leq\frac{22}{7}$ (by using intercept theorem for $\frac{\sqrt{7}}{7}$) and fully geometrical solving this time: enter image description here

Krzysztof Myśliwiec
  • 201
0

Topic: Radius $\sqrt{\pi}$

Today (and this gonna be my last post- unless I get requests) with the golden ratio:

$\phi=\frac{1+\sqrt{5}}{2}$ ; Property : $\phi^2=\phi+1$

I found this pythagorean relation: $$ (\sqrt{\pi})^2\leq\phi^2+(\frac{\phi}{4})^2+0.6^2 $$ enter image description here Accuracy: $$$$ \begin{align} \frac{17}{16}\phi^2+0.36\approx3.141661\\ \pi\approx3.141593 \\ { For-comparison:} \frac{22}{7}\approx3.14\color{red}{2857} \\ \end{align}

Krzysztof Myśliwiec
  • 201