1

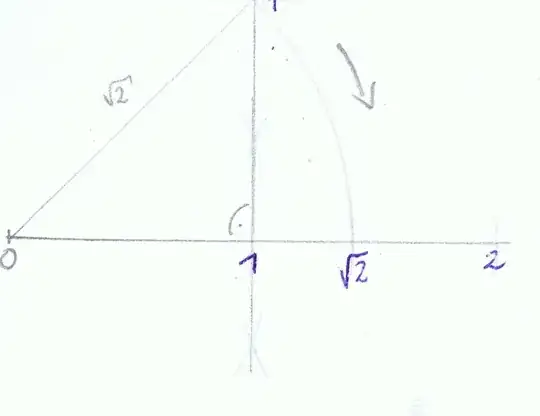
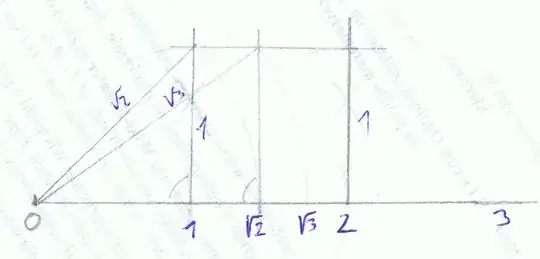
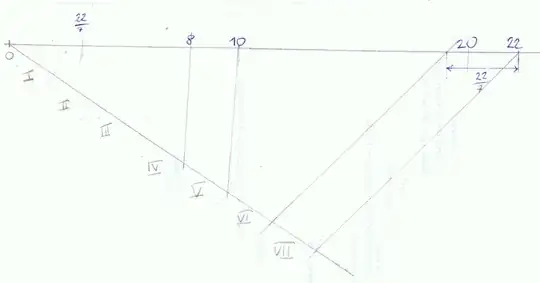
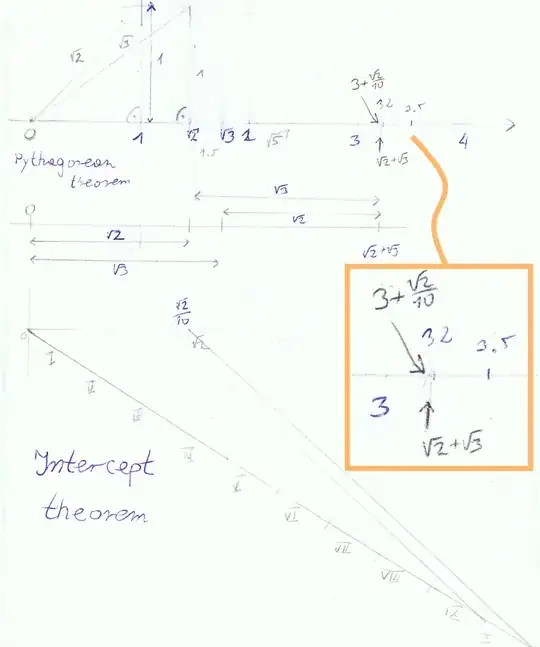
If we construct a square with side length 1, take its diagonal length : $\sqrt{2}$

However I still don't understand HOW it can lie on the number line.

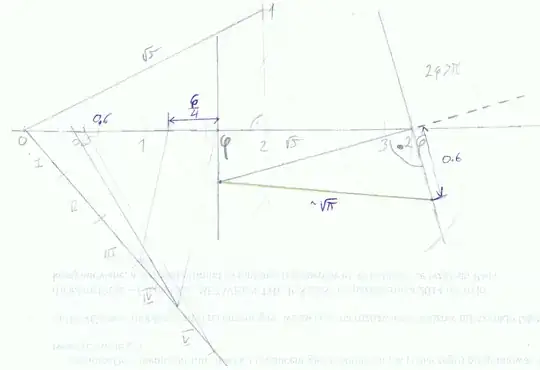
Imagine another irrational number $\pi = 3.1415926535...$

This number is also construct-able, and thus lies successfully on the number line.

However, for such a number to "lie" on the number line, it should be stationary.

If we look at the number $\pi$

$\pi = 3.1...$ We know $3.1 < \pi <3.2$

$\pi = 3.14...$ We know $3.14 < \pi <3.15$

$\pi = 3.141...$ We know $3.141 < \pi <3.142$

$\pi = 3.1415...$ We know $3.1415 < \pi <3.1416$

This list would go on forever, and the number $\pi$ is always "in-between" the two values,

$a < \pi < b$

and thus always in an increment (non-stationary) of a tiny value, compared to $a$.

Bart Michels
  • 26,355
VladeKR
  • 433
  • 2
    Notice that $4.999 < 5 < 5.001$, as is $4.9999 < 5 < 5.0001$. We can make that go on forever--why is $5$ on the number line? – apnorton Oct 23 '14 at 19:23
  • Consider those increments around $\pi$, the point that is common to all of them is the number $\pi$. – Benjamin Oct 23 '14 at 19:23
  • $1/3 = 0.3...$ We know $0.3 < 1/3 <0.34$

    $1/3= 0.33...$ We know $0.33 < 1/3 <0.334$

    $1/3 = 0.333...$ We know $0.333 < 1/3 <0.334.$

    Yet $1/3$ is rational, so it also doesn't lie on the real line.

     – Alex R. Oct 23 '14 at 19:27
  • @anorton That should be an answer. – Jack M Oct 23 '14 at 19:27
  • 1
    You are observing that the rationals are dense in the reals. But then so are the irrationals, because even starting with one single irrational (your $\pi$ or your $\sqrt{2}$) you can scoot it around by all possible rational displacements to get a dense set of irrationals ${\pi + q : q\in\mathbb Q}$. In fact, it's much worse than that. There are only a countable number of rationals, and everything else is irrational (we only use one irrational and its rational translates above). So "most" of the reals are irrational. – MPW Oct 23 '14 at 19:29
  • @anorton Yes I agree, but those numbers are predictable, 4.999n, we know that that "n" will be a 9. For irrational number though, we do not know that "n" because there's no periodicity. – VladeKR Oct 23 '14 at 19:43
  • @VladeKR I contend that the numbers to the right/left of $\pi$ are also predictable--precisely $\pi - 10^{-n} < \pi < \pi + 10^{-n}$. :) Really, though--there's no requirement for a real number to be predictable. – apnorton Oct 23 '14 at 19:45
  • So I'm kinda guessing it's a sandwich theorem where $a<x<b$ and when $a=b$ then $x=a=b$. – VladeKR Oct 23 '14 at 19:52

4 Answers4

2

Your question basically boils down to how do we know that the real numbers are complete, because like you said you can come up with smaller and smaller intervals with rational endpoints that contain your irrational number. If the real numbers are complete, then the intersection of all these intervals will be a single point, your number. There are multiple formal constructions of the real numbers starting with the rationals (Dedekind cuts are one) and you can prove the real numbers are indeed complete based on the construction. So all your limits of convergent sequences exist as a real number.

user2566092
  • 26,142
1

From Wikipedia:

"Cantor published ... a paper defining irrational numbers as convergent sequences of rational numbers"

http://en.wikipedia.org/wiki/Georg_Cantor

What you are observing is precisely one definition of irrational numbers; they are the numbers that "fill in" all the "gaps" between the rationals.

graydad
  • 14,077
  • Did not realize that Cantor strongly influenced Dedekind's construction of the reals as Dedekind cuts. Thanks for that interesting factoid. – user4894 Oct 23 '14 at 19:27
0

Tools: Ruler, compass and pencils

I. Pythagorean theorem (only)

I.1.How to lie $\sqrt{2}$: enter image description here I.2. Step I.1. is required to create $\sqrt{3}$ enter image description here Next are $\sqrt{4}=2$; $\sqrt{5}$;$\sqrt{6}$...

Recursion is not required by starting $\sqrt{1^2+1^2}$- roots like $\sqrt{19}$ can be create from $\sqrt{4^2+(\sqrt{3})^2}$

I.3. Set $\pi$ as approximation of $\pi^2$: $$ \pi^2\leq 0.1^2+0.5^2+3.1^2 $$ enter image description here II. The next important theorem to pythagorean is the intercept theorem

II.1. An example on $\frac97$: enter image description here II.2. An approximation for $\pi\approx\frac{22}{7}$:

Sample way 1: enter image description here Sample way 2: enter image description here III. Combine both theorem- Interval $\pi$: $$3+\frac{\sqrt{2}}{10}<\pi<\sqrt{2}+\sqrt{3}$$ enter image description here

IV. Bonus: the golden ratio $\phi$ (and $2\phi$) I have draw (for here):$\phi=\frac{1+\sqrt{5}}{2}$ enter image description here

Krzysztof Myśliwiec
  • 201
0

A number is not the same as the sequence that has it as a limit; i.e. it is "stationary" even if one has to use an infinite sequence of rational numbers to get it as a limit.

The reason why it might be difficult to visualize irrational real numbers is because the rationals are dense; i.e. for any two rational numbers there is another rational number lying in between. So, in some sense, the "rational line" would appear exactly the same as the real line, except that it is not a complete line in the sense that limits are lacking from it.

The canonical construction of the real numbers is in terms of Dedekind cuts. Take our "rational line" and arbitrarily partition it into two parts, such that the right set has no smallest element. Then it is possible that the left set has no smallest element either, and we've produced a gap that must be filled with the irrationals. With the real numbers, there is no way to produce such a gap; any cut on the real line must have either a greatest element in the left set or a smallest element in the right side. Can you see why this is the case?

Marc
  • 965
  • 4
  • 13