Area of square under a curve.

Question

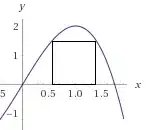
A square having sides parallel to the coordinate axes is inscribed in the region.
{$(x,y):x,y>0:y\le -x^3+3x$}.
If the area of the square is written as $A^{1/3}+B^{1/3}$ square units where $A,B\in \Bbb Z$ and $A>B$, then find
(i)$\sqrt{A-B}$
(ii)Slope of line with x and y intercepts as $A,B$ respectively
(iii)$A+B\over A-B$
(iv)Circumradius of $\triangle OPQ$ where $O$ is origin, $P(A^{1/3},0)$ and $Q(0,B^{1/3})$

My approach:
Let the square be $KLMN$ where $K,L$ lie on x-axis with coordinates $(a,0);(b,0)$ respectively.
This will give coordinates of other points i.e. $M,N$ in terms of $a,b$.
Now taking out the length of all sides and equating them will give $a,b$.

Problem with my approach:
I end up in a cumbersome equation involving $a,b$

Tips: I know nothing more than simple differentiation and limits. So please avoid solutions with integration and other stuffs.

PS: No need to downvote as I'm on the verge of getting banned. Please comment if you have any problem with the question.

I would just find the point at which x and y are equal on the curve. Then you have the area as x*y. Am I missing something? — poetasis, May 22 '18 at 16:54
I think yes. That square is inscribed in the region of curve in 1st quadrant. So how can you find area like that?? — Love Invariants, May 22 '18 at 16:59
@JohnGlenn Judging from the graph, there's only one possible inscribed square. — Ѕᴀᴀᴅ, Jun 01 '18 at 15:39

John Glenn · Answer 1 · 2018-06-02T03:16:07.927

1

Define $f(x):=3 x - x^3$. Obviously, the square must have a side length of $f(q)$, and we need to find $q$ that gives the largest square inside $f(x)$.

The line $y=f(q)$ intersects $y=f(x)$ at three points: $$\left(q,f\left(q\right)\right)\\ \left(\frac{1}{2} \left(-\sqrt{3} \sqrt{4-q^2}-q\right),f\left(\frac{1}{2} \left(-\sqrt{3} \sqrt{4-q^2}-q\right)\right)\right)\\ \color{red}{\left(\frac{1}{2} \left(\sqrt{3} \sqrt{4-q^2}-q\right),f\left(\frac{1}{2} \left(\sqrt{3} \sqrt{4-q^2}-q\right)\right)\right)}\\ $$

We are only interested at the last point. The top left vertex of the square is $(q,f(q))$, and we need to ensure that $\sqrt{(f(q)-f(z))^2+(q-z)^2}=f(q)$, where $z=\frac{1}{2} \left(\sqrt{3} \sqrt{4-q^2}-q\right)$. So we need to find $q$ for the equation below: $$\sqrt{(f(q)-f(z))^2+(q-z)^2}-f(q)=0\tag{1}$$

You can use this implementation to get the intuition for the solution.

This gives us two solutions: $$\left\{\left\{q\to \sqrt{1+\sqrt[3]{2}}\right\},\left\{q\to \sqrt{3-\sqrt[3]{2}-2^{2/3}}\right\}\right\}$$ Which means the area of the maximum square is: $$\bbox[5px,border:2px solid black]{f(q)^2 \iff f\left(\sqrt{3-\sqrt[3]{2}-2^{2/3}}\right)^2=6-3\times 2^{2/3}}$$

To get $A$ and $B$ set: $$A^{1/3}=6\iff A=6^3=216\\ B^{1/3}=3\times2^{2/3} \iff B=(3\times2^{2/3})^3=108$$ Since $\sqrt[3]A+\sqrt[3]{-B}=\sqrt[3]A-\sqrt[3]{B}$, for reals, we have the solution: $$\therefore{A=216\\B=-108}$$

The questions can now be easily answered:

$\sqrt{216+108}=\sqrt{324}=18$
Line passes through $(216,0)$ and $(0,-108)$, therefore: $y=\frac{-108}{216}(x-216)\iff y=\frac12x+108$
$\frac{108}{324}=\frac13$
The circumcircle is centered at: $$\left(\frac62,-\frac{3\times2^{2/3}}{2}\right)$$ therefore the radius is $$r=\sqrt{3^2+\left(-\frac{3\times2^{2/3}}{2}\right)^2}=\sqrt{9+\frac{9}{2^{2/3}}}=\frac{3 \sqrt{1+2^{2/3}}}{\sqrt[3]{2}}$$

edited Jun 02 '18 at 03:16

answered Jun 01 '18 at 14:37

John Glenn

2,323
11
25

It came in an exam which allows no calculator to students. Also I specifically mentioned manual approaches are only applicable. – Love Invariants Jun 01 '18 at 15:12
It is mentioned in the description below the question – Love Invariants Jun 01 '18 at 15:15
Also your values for $A$ and $B$ are wrong. Answer has $A=216$ and $B=-108$ – Love Invariants Jun 01 '18 at 15:23
From the answer it is quite evident that this question is solvable without calculator – Love Invariants Jun 01 '18 at 15:28
Actually, given we now have the area. This is actually easily solvable. Let me edit my answer. – John Glenn Jun 01 '18 at 15:33
How did you arrive at the values of q? – Love Invariants Jun 01 '18 at 18:14
As pointed out you just solve the equation. Since the height of the square is always $f(q)$, then you need to find the largest possible width $f(q)$. You just use the distance formula and set that equal to $f(q)$ (using the top left and right vertices of the square). – John Glenn Jun 02 '18 at 02:46
You just have to solve for $q$ in $(1)$ – John Glenn Jun 02 '18 at 03:17
Hi. How did you solve for q in (1)? Isn't that cumbersome? Can that be solved by hand? – aarbee Aug 18 '22 at 18:06

score 1 · Accepted Answer · answered Jun 01 '18 at 18:40

1

There have to be reasons if you are "on the verge of getting banned". E.g., we are not given any hint as to the source of this quite involved problem. Anyway, this problem is of a purely algebraic nature. Please don't write "$P(A^{1/3},0)$" when you mean "$P=(A^{1/3},0)$". No function $P$ of two variables is defined in the actual context.

The problem obviously has exactly one solution $(a,b)$. It is therefore sufficient to argue about necessary conditions for $a$ and $b$.

The quantities $a\ne b$ satisfy $$b-a=a(3-a^2),\qquad b-a=b(3-b^2)\ .\tag{1}$$ Subtracting these equations we obtain $0=(b-a)(3-a^2-ab-b^2)$, hence $$3-a^2-b^2=ab\>,\quad{\rm resp.,}\quad (a+b)^2=3+ab\ .\tag{2}$$ Adding the equations $(1)$ leads together with $(2_1)$ to $$2(b-a)=(a+b)(3-a^2+ab-b^2)=2(a+b)ab,$$ hence $b-a=(a+b)ab$. Squaring this we obtain $(b-a)^2=(a+b)^2(ab)^2$, hence $$(a+b)^2-4ab=(a+b)^2(ab)^2\ ,\tag{3}$$ and together with $(2_2)$: $$3(1-ab)=(3+ab)(ab)^2\ .$$ Now this is saying that $(ab+1)^3=4$, hence $z:=ab=2^{2/3}-1$. Now $(3)$ gives $$(a+b)^2={4z\over1-z^2}$$ and therefore $$(b-a)^2=(a+b)^2-4ab={4z^3\over1-z^2}=6-3\cdot2^{2/3}=\root3 \of{216}-\root3\of {108}\ .$$ It follows that $A=216$ and $B=-108$. The rest is easy.

answered Jun 01 '18 at 18:40

Christian Blatter

226,825

$(A,B)=(216,-108)$ gives the area $$S\approx\color{red}{1.237796}$$ but $(A,B)=(68,-23)$gives $S\approx\color{red}{ 1.237788}$ and $(A,B)=(121,-51)$ gives $S\approx \color{red}{1.2377657}$.
My answer has been blocked, I can not publish it (I wonder why) – Piquito Jun 01 '18 at 23:49
@Piquito those other values will not give the exact value of the area. – John Glenn Jun 02 '18 at 02:49
@ChristianBlatter- thx. Most of the questions here dont have source. This question was given in my textbook book which contains only questions and isn't available in market(only to students of my institution). Its questions are collection of problems from previous exams – Love Invariants Jun 02 '18 at 07:21
@John Glenn: I know. What I wanted to say is that because of $a$ is an irrational of degree six (root of the irreducible $x^6-9x^4+21x^2-3=0$) if someone walk by this road, then no way to determine the exact values of $A$ and $B$ without calculator as ask the OP. No more, just this. Regards. – Piquito Jun 02 '18 at 11:55

Area of square under a curve.

2 Answers2