Understanding the use of convolution in neural networks.

Question

I'm reading about Convolutional Neural Networks (CNNs) in Deep Learning by Ian Goodfellow.

CNNs are different from traditional neural networks in that they use convolution in place of general matrix multiplication in at least one of their layers. The convolution is introduced as follows:

Suppose that we are tracking the location of a spaceshift with a laser sensor. Our laser provides a single output $x(t)$, the position of the spaceship at time $t$. Both $x$ and $t$ are real-valued, that is, we can get a different reading from the laser sensor at any instant in time. Now suppose our laser is somewhat noisy. To obtain a less noisy estimate of the spaceship's position, we would like to average several measurements. Of course, more recent measurements are more relevant, so we will want this to be a weighted average that gives more weight to recent measurements. We can do this with a weighting function $w(a)$, where $a$ is the age of a measurement. If we apply such a weighted average operation at every moment, we obtain a new function $s$ providing a smoothed estimate of the position of the spaceship: $$\displaystyle s(t) = \int x(a)w(t - a)da$$ This operation is called convolution

$\ldots$

In convolutional network terminology, the first argument (in this example, the function $x$) to the convolution is often referred to as the input, and the second argument (in this example, the function $w$) as the kernel. The output is sometimes referred to as the feature map.

$\ldots$

In machine learning applications, the input is usually a multidimensional array of data, and the kernel is usually a multidimensional array of parameters that are adapted by the learning algorithm. We will refer to those multidimensional arrays as tensors. Because each element of the input and kernel must be explicitly stored separately, we usually assume that these functions are zero everywhere but in the finite set of points for which we store the values. This means that in practice, we can implement the infinite summation as a summation over a finite number of array elements. Finally, we often use convolutions over more than one axis at the time. For example, if we use a two-dimensional image $I$ as our input, we probably also want to use a two-dimensional kernel $K$: $$S(i,j) = (I*K)(i,j) = \sum_m\sum_nI(m,n)K(i-m,j-n)$$

(I assume that $S(i,j)$ means the feature map at point $(i,j)$).

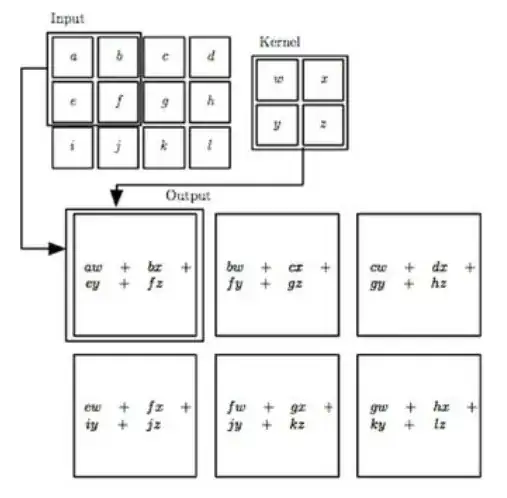
The author then gives an example of $2$-D convolution with the following image:

I don't understand how this image illustrates what the author explains earlier. If we consider the input an image, then $a$ would resemble $I(0,0)$ right? Using the given definition of the feature map I find that $S(0,0) = \sum_m\sum_nI(m,n)K(0-m,0-n) = I(0,0)K(0,0) = aw$. Since e would resemble $I(1,0)$ I find that $$S(1,0) = \sum_m\sum_nI(m,n)K(1-m,0-n) = I(0,0)K(1,0) + I(1,0)K(0,0) = ay + ew$$ However, according to the image the output would be $aw + bx + ey + fz$.

Question: Why does the output equal $aw + bx + ey + fz$?

Edit: If the displayed outputs (feature maps) are only the outputs corresponding to the internal points on the grid, then I think I understand the figure. I would mean that the highlighted output corresponds to $S(1,1)$ and that the outputs $S(0,0), S(1,0), \ldots$ are simply not shown here right?

Thanks in advance!

Answer 1

Unfortunately, it is common practice in machine learning to compute correlations rather than convolutions (but calling them convolutions). They are different: for instance, see [1], [2], [3], [4], [5]. In the 2D case: \begin{align} \text{Corr: }\; C(u,v) &= (f\star g)(u,v)=\iint_{\mathbb{R}^2} f(u,v) g(u+x,v+y) \;dx dy\\ \text{Conv: }\; H(u,v) &= (f\ast g)(u,v)=\iint_{\mathbb{R}^2} f(u,v) g(u-x,v-y) \;dx dy \end{align} So notice that one can compute a convolution by mirroring the filter kernel (i.e., flipping vertically and horizontally) and then computing a correlation. So the answer to your question is just to do that double flipping first.

This renaming of correlations vs convolutions has seemingly caused widespread confusion. E.g., see these posts: [1], [2], [3], [4], [5], [6]. So why has it happened? Basically because (1) correlation and convolution have equal representational power (i.e., the capacity of a model using one is equal to that of a model using the other), (2) the kernels are learned so whether it is mirrored or not makes no difference, and (3) because convolution has such nice properties (e.g., Convolution Theorem for Fourier transforms) and is classically/historically more important in computer vision, practitioners prefer to think in terms of convolutions.