How to draw subgroup lattice for extension field $\mathbb{Q}(\sqrt[4]{2},i)$
It seems obvious that
$$\mathbb{Q}(\sqrt[4]{2}), \mathbb{Q}(\sqrt{i}) \subset \mathbb{Q} (\sqrt[4]{2},i)$$
and $$\mathbb{Q} (\sqrt{2}) \subset \mathbb{Q} (\sqrt[2]{2}) \subset \mathbb{Q} (\sqrt[4]{2})$$
is there a systematic way to find the diagram below?
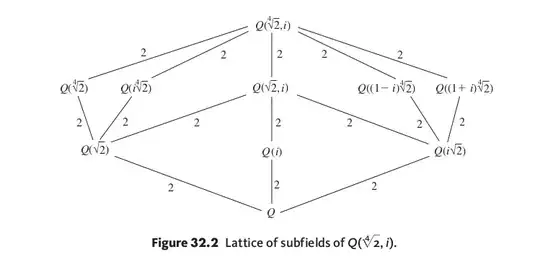
You can use the Galois Correspondence. Let $L = \mathbb{Q}(\sqrt[4]{2},i)$. After a bit of calculation you should be able to conclude that $\text{Gal}(L/\mathbb{Q}) \cong D_4$, the dihedral group on $4$ elements. In fact let:
$$Id : \begin{array}{lr} \sqrt[4]{2} \to \sqrt[4]{2}\\ i \to i \end{array}\quad \quad \tau: \begin{array}{lr} \sqrt[4]{2} \to i\sqrt[4]{2}\\ i \to i \end{array} \quad \quad \sigma: \begin{array}{lr} \sqrt[4]{2} \to \sqrt[4]{2}\\ i \to -i \end{array}$$
Then $\text{Gal}(L/\mathbb{Q}) = \{Id,\tau,\tau^2,\tau^3,\sigma,\tau\sigma,\tau^2\sigma,\tau^3\sigma\}$. Now by Galois Correspondence we have that each subgroup of $\text{Gal}(L/\mathbb{Q})$ corresponds to a subfield of $L$, containing $\mathbb{Q}$. Moreover the index of the subgroup will give you the extension degree over $\mathbb{Q}$.
To explicitly determine the fixed fields by subgroups of $\text{Gal}(L/\mathbb{Q})$ we apply it to a general term written in the basis. For example take $H = \{Id, \tau\sigma\}$. Then we have that:
$$\tau\sigma\left(a+b\sqrt[4]{2}+c\sqrt[4]{2^2} + d\sqrt[4]{2^3} + ei + fi\sqrt[4]{2} + gi\sqrt[4]{2^2} + hi\sqrt[4]{2^3}\right) = $$ $$\tau\left(a+b\sqrt[4]{2}+c\sqrt[4]{2^2} + d\sqrt[4]{2^3} - ei - fi\sqrt[4]{2} - gi\sqrt[4]{2^2} - hi\sqrt[4]{2^3}\right) =$$ $$a+bi\sqrt[4]{2}-c\sqrt[4]{2^2} - di\sqrt[4]{2^3} - ei + f\sqrt[4]{2} + gi\sqrt[4]{2^2} - h\sqrt[4]{2^3}$$
So we get that $a,g,b,d$ are free, $h=-d, f=b, e=c=0$. So the fixed field of $H$ is:
$$L_H = \{a + b(1+i)\sqrt[4]{2} + gi\sqrt[4]{2^2} + d(1-i)\sqrt[4]{2^3} \mid a,b,g,d \in \mathbb{Q}\} = \mathbb{Q}((1+i)\sqrt[4]{2})$$
In general we have the following correspondence:
$$G \longleftrightarrow \mathbb{Q}$$ $$\{Id,\tau,\tau^2,\tau^3\} \longleftrightarrow \mathbb{Q}(i)$$ $$\{Id,\sigma, \tau^2, \tau^2\sigma\} \longleftrightarrow \mathbb{Q}(\sqrt{2})$$ $$\{Id,\tau\sigma, \tau^2, \tau^3\sigma\} \longleftrightarrow \mathbb{Q}(i\sqrt{2})$$ $$\{Id,\tau^2\} \longleftrightarrow \mathbb{Q}(\sqrt{2},i)$$ $$\{Id,\sigma \} \longleftrightarrow \mathbb{Q}(\sqrt[4]{2})$$ $$\{Id,\tau\sigma\} \longleftrightarrow \mathbb{Q}((1+i)\sqrt[4]{2})$$ $$\{Id,\tau^2\sigma\} \longleftrightarrow \mathbb{Q}(i\sqrt[4]{2})$$ $$\{Id,\tau^3\sigma\} \longleftrightarrow \mathbb{Q}((1-i)\sqrt[4]{2})$$ $$\{Id\} \longleftrightarrow \mathbb{Q}(\sqrt[4]{2},i)$$
Then just draw the subgroup lattice of $\text{Gal}(L/\mathbb{Q})$ and just flip it and write the corresponding fields to get the field lattice.
