Must a monotone function have a monotone derivative?

Question

If a function is differentiable and monotone on the interval $(a, b)$, then its derivative is also monotone on $(a, b)$.

How do you prove this statement is wrong?

Can you please provide an example?

score 71 · Answer 1 · answered Jan 13 '13 at 20:23

71

This thing

${}{}{}{}{}{}{}{}{}{}{}{}{}{}{}$

answered Jan 13 '13 at 20:23

MJD

65,394
39
298
580

36

It's 2-valued at one interval. Need eraser. – alancalvitti Jan 13 '13 at 20:24
6

We need more pictures on MSE :) – countunique Jan 13 '13 at 21:21

score 21 · Answer 2 · answered Jan 13 '13 at 20:21

21

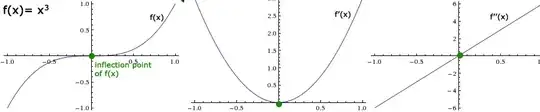
Consider $f(x)=x^3$ on $[-1,1]$. Then it is clearly monotone, but $f'(x)=3x^2$ which is clearly not monotone.

answered Jan 13 '13 at 20:21

Clayton

24,751

11

Google search has improved! search for x^3, 3*x^2 – user13107 Jan 14 '13 at 01:16

Max Malysh · Answer 3 · 2013-10-14T17:33:44.903

No, it shouldn't.

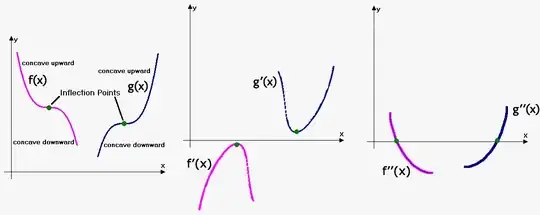
Explanation of this fact can be based on the convexity of the function, which depends on the second derivative of the function.

In other words: if the function is monotone on some interval, as well as its derivative, the function doesn't have point(s) of inflection. In case the function is monotone, but its derivative is not, the function has point(s) of inflection on the interval.

When function is monotone, but its derivative is not, function changes type of its convexity still being monotone. Of course, this happens in the case if the necessary convexity condition is true.

Several people have already posted $x^3$ as example. Here are some plots: the function and its first and second derivatives.

$x^3$

Another example:

random function

+1 for a general explanation instead of just a counter-example — Kevin, Jan 14 '13 at 07:31

score 5 · Answer 4 · answered Jan 13 '13 at 20:21

5

$f(x)=x^3$, with $-1<x< 1$.

answered Jan 13 '13 at 20:21

Git Gud

31,356

score 5 · Answer 5 · answered Jan 13 '13 at 20:42

Just for another example $f(x)=x^3+x$ has non-zero derivative $3x^2+1$.

The only thing you need for $f(x)$ to be increasing is for the derivative to be non-negative (and if you want strictly increasing you need zeros of the derivative to be isolated). Take your favourite wiggly non-negative function (not too pathological) and integrate it - eg $\sin^2 x$.

score 1 · Answer 6 · answered Jun 21 '19 at 02:17

Can we take a non-monotone function whose derivative is bounded non-monotone and modify it so that the function remains monotone and the derivative remains non-monotone? Yes, adding a constant to the derivative larger than minus its lower bound leaves the derivative non-monotone but makes the function monotone.

Example? Sine is non-monotone with a bounded non-monotone derivative. Minus the lower bound of the derivative is $1$ and one of its antiderivatives is $x$. So $f(x) = x + \sin x$ is monotone because its derivative is non-negative. (This is not strictly monotone. If we want strict monotony, increase the derivative by $1+\varepsilon$ for any $\varepsilon > 0$.) And its derivative has only been vertically shifted, so is non-monotone.

Must a monotone function have a monotone derivative?

6 Answers6

Linked

Related