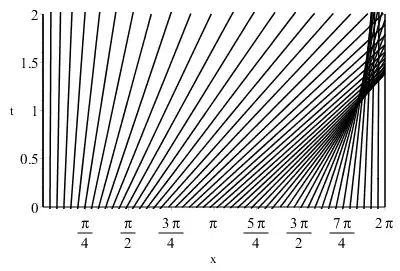
I'm trying to solve numerically the inviscid Burgers' equation $u_t + u u_x = 0$ with the method of characteristics. Most of all, I want to see how the numerical solution gets "multiple-values" for times $t>1$ as shown here in figure 3.5.
The initial condition is $u(x,0)=1-\cos(x)$ for $x \in [0,2\pi]$
I wanted to use central finite differences and Euler's method.
The discretized equation becomes $$u'(t)=-u_i(t) \cdot \frac{u_{i+1}(t)-u_{i-1}(t)}{2h} .$$ Now the PDE has become an ODE and I'll use Euler's method, as done in the following runable MatLab code:
mx=100; %number of nodes in x
x=linspace(0,2*pi,mx)';
h=(2*pi)/mx; %step size
mt=200; %number of time steps
tend=1.5; %final time
k=tend/mt; %step
%Build the matrix of finite centered differences
B = toeplitz(sparse(1,2,-1/(2*h),1,mx),sparse(1,2,1/(2*h),1,mx));
%initial condition
u0=@(x) 1-cos(x);
u=NaN(mx,mt+1);
u(:,1)=u0(x);
t=0;
for n=1:mt
u(:,n+1)=u(:,n) - k*(u(:,n).*(B*u(:,n))); %Euler's method
t=t+k; %update the current time
plot(x,u(:,n))
axis([0,2*pi,0,7])
title(sprintf('t = %0.2f',t));
xlabel('x')
ylabel('u(t,x)')
pause(0.01)
end
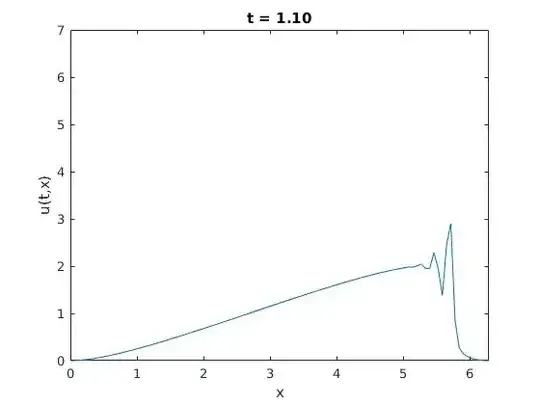
This code produces a plot for each time $t$, where I can't see a multi-valued solution! I just see that things go bad for $t>1$, as expected. In fact, for $t \approx 1.1$, I got the following graphic:
Maybe the problem is that I'm using forward Euler, which is not a good choice?
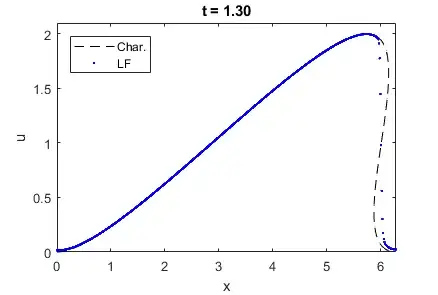
g = @(x) 1-cos(x); t=1.3; plot(x+t*g(x), g(x));should work for one plot, it should then be easy to write a loop fortaround it. – Lutz Lehmann May 02 '18 at 16:16