Find the breaking time in IVP for classical Burgers equation

Question

Consider Burgers equation $u_t+uu_x=0$, such that $$ u(x,0)=\phi(x)=\left \{\begin {array}{lll} 2, & x\leq \pi/2\\ \sin x+1, & \pi/2\leq x \leq 3\pi/2\\ 0, & x \geq 3\pi/2\\ \end{array} \right.. $$

Find the breaking time $t_B.$

Attempt. We easily get the characteristic curves $x=\phi(r)t+r$ ($r$ parameter). So:

for $r<\pi/2$ we get $x=2t+r,$

for $\pi/2<r<3\pi/2$ we get $x=(\sin r+1)t+r$ and

for $r>3\pi/2$ we get $x=r.$

The "limit" curves $x=2t+\pi/2$ and $x=3\pi/2$ meet at time $\pi/2$, and also the curve $x=(\sin \pi+1)t+\pi=t+\pi$ meets the above at time $\pi/2$. On the other hand though, the curve $$\displaystyle x=\Big(1+\frac{1}{\sqrt{2}}\Big)t+\frac{5\pi}{4}$$meets $x=t+\pi$ and some time $<\pi/2$. So, how can I find the minimum of the times these curves intersect?

Thanks in advance!

Answer 1

The initial data $u(x,0) = \phi(x)$ is continuously differentiable, with derivative $$ \phi'(x) = \left\lbrace \begin{align} &0 && \text{if}\quad x\leq \pi/2 \, ,\\ &\cos x && \text{if}\quad \pi/2\leq x \leq 3\pi/2 \, ,\\ &0 && \text{if}\quad 3\pi/2 \leq x \, . \end{align} \right. $$ In the case of Burgers' equation $u_t + u u_x = 0$, the time $t_B$ at which a shock occurs (or the minimal time where characteristic curves intersect) is given by (1) $$ t_B = \frac{-1}{\min \phi'(x)} = 1 \, . $$ This is illustrated in @JJacquelin answer, and in the following sketch of the $x$-$t$ plane:

---

Note : cf. exercise 3.3. of

(1) R.J. LeVeque, Numerical Methods for Conservation Laws. Birkhäuser, 1992.

Answer 2

This is a partial answer, hoping it will help :

FIRST PART : Solving $\quad u_t+uu_x=0\quad $without taking account of the initial conditions.

Set of characteristic differential equations : $\quad \frac{dt}{1}=\frac{dx}{u}=\frac{du}{0}$

A first equation of characteristic curve comes from $du=0\quad\to\quad u=c_1$

A second equation of characteristic curve comes from $\quad \frac{dt}{1}=\frac{dx}{c_1} \quad\to\quad x-c_1t=c_2$

General solution on the form of an implicit equation : $$\Phi\left(c_1\:,\:c_2\right)=\Phi\left(u\:,\:x-ut\right)=0$$ where $\Phi$ is any differentiable function of two variables. An equivalent form is : $$u=F\left(x-ut\right)$$ where $F$ is any differentiable function of one variable.

SECOND PART :

Particular solution with regard to the initial condition $\quad u(x,0)=\phi(x)$ $$u(x,0)=F(x+0u)=F(x)=\phi(x)$$ $$u(x,t)=\phi(x-ut)$$ The function $\phi$ is defined as : $\quad \begin{cases} \phi(\theta)=2\qquad\text{if } \quad \theta \leq \frac{\pi}{2}\\ \phi(\theta)=\sin(\theta)+1 \qquad\text{if }\quad \frac{\pi}{2}\leq \theta \leq \frac{3\pi}{2}\\ \phi(\theta)=0\qquad\text{if } \quad \frac{3\pi}{2}\leq\theta \end{cases}$

We introduce a dummy variable $\theta$ in order to not confuse $x$ when $t=0$ with $(x-ut)$ when $t\neq 0$.

Thus the solution is : $$\quad \begin{cases} u=2\qquad\text{if } \quad (x-ut) \leq \frac{\pi}{2}\\ u=\sin(x-ut)+1 \qquad\text{if }\quad \frac{\pi}{2}\leq (x-ut) \leq \frac{3\pi}{2}\\ u=0\qquad\text{if } \quad \frac{3\pi}{2}\leq(x-ut) \end{cases}$$

$$\quad \begin{cases} u=2\qquad\text{if } \quad x \leq 2t+\frac{\pi}{2}\\ u=\sin(x-ut)+1 \qquad\text{if }\quad ut+\frac{\pi}{2}\leq x \leq ut+\frac{3\pi}{2}\\ u=0\qquad\text{if } \quad x \geq\frac{3\pi}{2} \end{cases}$$

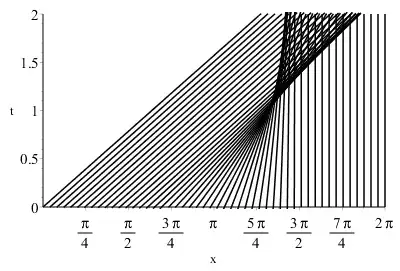
From this, it is possible to draw the curves $x(t)$ for various specified values of $u$.

Note that : $\quad 0\leq u\leq 2$

The figure below shows $u$ as a function of $x$ for various values of $t$ (Drawn from numerical calculus) :

$u=0$ for $t>\frac{2\pi}{3}$ and/or $x>\frac{2\pi}{3}$