Closed form for the integral $\int_0^{\pi/2} \frac{x-\sin x}{\tan x-x} dx$

Question

Can we find a closed form for the following integral (in terms of any known constants, elementary or special functions)? Numerical value obtained by Wolfram Alpha is:

$$I=\int_0^{\pi/2} \frac{x-\sin x}{\tan x-x} dx=0.51235905260998669767\dots$$

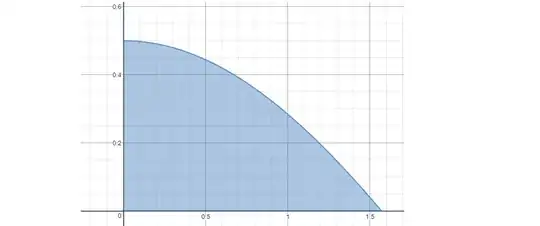
The function under the integral is very nice in the range of interest and looks like this:

---

What we know about the function under the integral:

$$f(x)=\frac{x-\sin x}{\tan x-x} $$

$$f(-x)=f(x)$$

$$\lim_{x \to 0} f(x)=\frac{1}{2}$$

$$\lim_{x \to 0} f'(x)=0$$

$$\lim_{x \to \pi/2} f(x)=0$$

$$\lim_{x \to \pi/2} f'(x)=1-\frac{\pi}{2}$$

---

The function is very closely approximated by its Taylor series (in the range of interest):

$$f(x)=\frac{1}{2}-\frac{9}{40}x^2+\frac{27}{2800}x^4-\frac{27}{112000}x^6+\cdots$$

This allows us to estimate the integral:

$$\frac{\pi}{4}-\frac{3}{320}\pi^3+\frac{27}{448000}\pi^5-\frac{27}{100352000}\pi^7 < I < \frac{\pi}{4}-\frac{3}{320}\pi^3+\frac{27}{448000}\pi^5$$

Or numerically (with correct digits highlighted):

$$\color{blue}{0.5123}4485141169155 < I < \color{blue}{0.51}315747016517901$$

---

Provided no closed form exists (which I find likely) can we find a different integral or series expression with general terms expressed in terms of known elementary or special functions?

---

We can also write:

$$I=\int_0^{\pi/2} \frac{\pi /2-x-\cos x}{\cot x+x-\pi/2} dx$$

Though, in this case I don't see how to use this.

---

Integrating by parts is hard, because for the obvious choices of $u$, we get divergence at $0$. Choosing the whole integrated function as $u$ makes the expression more complicated:

$$I=\int_0^{\frac{\pi }{2}} \frac{ x \left(1-\cos ^3 x\right)+\sin x \cos 2 x-\frac{1}{2} \sin 2 x}{(x \cos (x)-\sin (x))^2} x\, dx$$

---

Or maybe contour integration could work here? In this case it will involve logarithms, which I don't know how to deal with.

Putting $e^{i x}=z$ and choosing the contour to be a half of the unit circle (possibly, I'm not sure), we will have:

$$I=\frac{1}{4} \int_{-\pi/2}^{\pi/2} \frac{(2 i x -e^{ix}+e^{-ix})(e^{i x}+e^{-ix})}{e^{ix}-e^{-ix}-ix(e^{ix}+e^{-ix})} dx=\frac{1}{4i} \oint \frac{(2 z \log z-z^2+1)(z^2+1)}{(z^2-1-(z^2+1) \log z)z^2} dz$$

I have no idea what to do with logarithms, and it seems to me as the only singularity the function has inside the contour is at $z=0$.

Answer 1

Here's something that may be helpful or not:

$$\begin{align} \int_0^{\pi/2}\frac{x-\sin(x)}{\tan(x)-x}dx &=\int_0^{\pi/2}\frac{x\cot(x)-\cos(x)}{1-x\cot(x)}dx\\ &=\int_0^{\pi/2}(x\cot(x)-\cos(x))\sum_{n=0}^\infty x^n\cot^n(x) dx\\ &=\sum_{n=0}^\infty \int_0^{\pi/2}(x\cot(x)-\cos(x))x^n\cot^n(x) dx\\ &=\sum_{n=1}^\infty \int_0^{\pi/2} x^n\cot^n(x) dx-\sum_{n=0}^\infty \int_0^{\pi/2}x^n\cot^n(x)\cos(x) dx\\ \end{align}$$

This probably won't lead to a nice closed form, but it could lead to some good approximations. The first couple terms of the leftmost series are $$\int_0^{\pi/2} x\cot(x)dx=\frac{\pi\ln(2)}{2}$$ $$\int_0^{\pi/2} x^2\cot^2(x)dx=\pi\ln(2)-\frac{\pi^3}{24}$$ $$\int_0^{\pi/2} x^3\cot^3(x)dx=\frac{9\pi\zeta(3)}{16}+\frac{3\pi\ln(2)}{2}-\frac{\pi^3}{16}-\frac{\pi^3\ln(2)}{8}$$ and the first couple of terms of the rightmost series are $$\int_0^{\pi/2} \cos(x)=1$$ $$\int_0^{\pi/2} x\cot(x)\cos(x)=2G-1$$ $$\int_0^{\pi/2} x^2\cot^2(x)\cos(x)=4G+2-\frac{\pi^2}{2}$$ where $G$ is Catalan's constant.

Perhaps this can lead to a nice approximation?

NOTE: The (hard) integrals are courtesy of Wolfram. If you want to know how to do any of them, leave a comment and I'll get back to you when I figure them all out myself. :)

Answer 2

A short answer regarding the series expansion of the integral.

Let $\,\displaystyle a_{m,n}:=\int_0^{\frac{\pi}{2}}(\cos x)^m \left(\frac{x}{\sin x}\right)^n\,$ with $\,\,m,n\in\mathbb{N}_0\,$.

It’s $\enspace\displaystyle a_{0,0}=\frac{\pi}{2}\enspace$ , $\enspace\displaystyle a_{m,0}=\frac{\sqrt{\pi}}{2}\frac{\Gamma\left(\frac{m-1}{2}\right)}{\Gamma\left(\frac{m}{2}\right)}\enspace$ for $\enspace m>0\,$

and $\enspace\displaystyle a_{0,n}=I_n\enspace$ ( see my answer in Generalised Integral $I_n=\int_0^{\pi/2} \frac{x^n}{\sin ^n x} \ \mathrm{d}x, \quad n\in \mathbb{Z}^+.$ ) .

It's: $$\int\limits_0^{\frac{\pi}{2}}\frac{x-\sin x}{\tan x - x}dx = -\frac{\pi}{2} + \int\limits_0^{\frac{\pi}{2}}\frac{1-\cos x}{1-x\cot x}dx = -\frac{\pi}{2} + \sum\limits_{n=0}^\infty (a_{n,n} – a_{n+1,n}) $$

For $\,n\ge 1\,$ we have:

$$a_{n,n}=\int\limits_0^{\frac{\pi}{2}} (x\cot x)^n dx = \frac{\left(\frac{\pi}{2}\right)^{n+1}\cos\frac{\pi n}{2}}{n+1} +$$$$+\frac{n}{2}\sum\limits_{q=0}^n {\binom n q}\sum\limits_{l=0}^n \frac{\left(\frac{\pi}{2}\right)^l\sin\frac{\pi l}{2}}{2^l l!}\sum\limits_{j=0}^{n-1} \begin{bmatrix}n\\{j+1}\end{bmatrix}\sum\limits_{v=0}^j {\binom j v}(-q)^{j-v}\eta(n-l+1-v)$$

$$a_{n+1,n}=\int\limits_0^{\frac{\pi}{2}} (\cos x)(x\cot x)^n dx =$$ $$=\frac{n}{2}\sum\limits_{q=0}^{n+1} {\binom {n+1} q}\sum\limits_{l=0}^n \frac{\left(\frac{\pi}{2}\right)^l\cos\frac{\pi l}{2}}{l!}\sum\limits_{j=0}^{n-1} \frac{1}{2^j} \begin{bmatrix}n\\{j+1}\end{bmatrix}\sum\limits_{v=0}^j {\binom j v}(1-2q)^{j-v}\beta(n-l+1-v)$$

with the Stirling numbers of the first kind $\begin{bmatrix}n\\k\end{bmatrix}$ defined by $\displaystyle\sum\limits_{k=0}^n\begin{bmatrix}n\\k\end{bmatrix}x^k:=\prod\limits_{k=0}^{n-1}(x+k),$

and $\enspace\beta(s)$ := Dirichlet $\beta$ function, $\enspace\eta(s)$ := Dirichlet $\eta$ function, $\,\,$ and their analytical extensions which also can be read in my answer of the question Generalised Integral $I_n=\int_0^{\pi/2} \frac{x^n}{\sin ^n x} \ \mathrm{d}x, \quad n\in \mathbb{Z}^+.$