1

I'm studying linear algebra and, in particular, the concept of determinant. I've understood the determinant in 2 dimension, but in 3d i have not clear the concept of oriented volume. Can you explain me ?

Qwerto
  • 969
  • 6
  • 20
  • Do you understand the concept of oriented area in 2-D? – amd Apr 04 '18 at 06:19
  • Yes, i've understood it previously – Qwerto Apr 04 '18 at 06:38
  • This is a misnomer. The word "orientation" originally referred to bearings, but the orientation in the so-called "oriented volume" is actually just a sign, which is either $1$ or $-1$, but not bearings in higher-dimensional spaces. The determinant should be called a signed volume. I don't understand why so many textbook authors still cling to that "oriented" thing. They are doing their readers disservices. – user1551 Apr 04 '18 at 08:21

1 Answers1

1

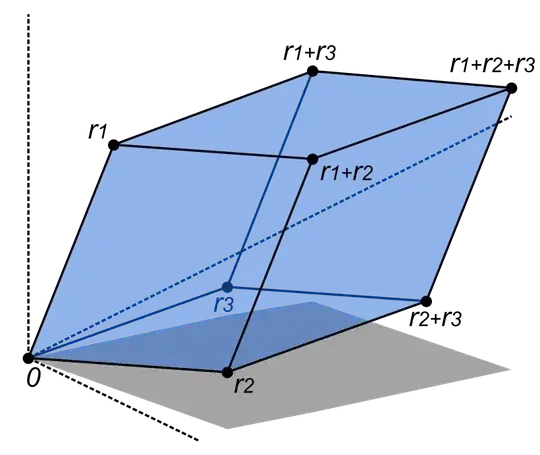
In 3d the absolute value of the determinant corresponds to the volume of the parallelepiped formed by the rows constructed from the vectors $r_1$, $r_2$, and $r_3$.

Since the determinant is equal to the triple product $$r_1\cdot (r_2\times r_3)$$ without absolute value the determinant can be negative or positive depending upon the orientation of the row vectors.

enter image description here

user
  • 154,566
  • More precisely, in the 3d case, what happens to the vectors that shape the parallelepiped when the sign of the determinant is negative ? – Qwerto Apr 05 '18 at 06:02
  • 1
    @Qwerto since $det(r_1,r_2,r_3)=r_1\cdot(r_2\times r_3)$ the sign depend by the direction of $r_2\times r_3$ with respect to $r_1$. In the figure here above $r_2\times r_3$ is up and thus $det(r_1,r_2,r_3)>0$ otherwise $det(r_1,r_3,r_2)$ is negative. See also there https://math.stackexchange.com/questions/314275/scalar-triple-product-why-equivalent-to-determinant – user Apr 05 '18 at 06:52