The area is very much a concept belonging to Calculus. In this regard to find the area of something without using Calculus is almost an oxymoron, but we can have an intuitive (and not too general) notion of area based on the following points:
- Any rectangle deserves an area (i.e. it is a measurable set) and the area of a rectangle $R$ with side lengths $a,b,a,b$ is $\mu(R)=ab$;
- Isometric measurable sets have the same area and if a line splits some measurable set $R$ into two components $R_1,R_2$ then $R_1,R_2$ are measurable and $\mu(R_1)+\mu(R_2)=\mu(R)$. This fixes the area of parallelograms, triangles, bounded polygons;
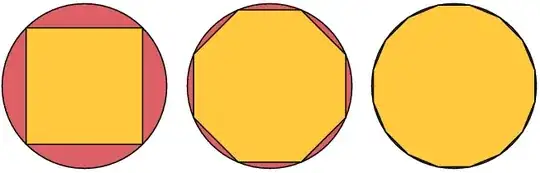
- Not every compact subset of $\mathbb{R}^2$ is a polygon, so we want to extend the notion of measurability in the following way: given $K$, a compact and connected subset of $\mathbb{R}^2$, we define $\mathcal{I}$ as the family of polygons contained in $K$, $\mathcal{E}$ as the family of polygons containing $K$. If
$$ \sup_{P\in\mathcal{I}} \mu(P) = \inf_{P\in\mathcal{E}}\mu(P) = L $$
we say that $K$ is measurable and define its area as $\mu(K)=L$.
Notice that 1.,2.,3. do not allow to measure unbounded sets like $\{(x,y)\in\mathbb{R}^2: x\geq 0, 0\leq y\leq\frac{1}{(x+1)^2}\}$
or subsets of $\mathbb{R}^2$ with countable connected components, like $\bigcup_{n\in\mathbb{N}}\{(x,y): (x-n)^2+y^2\leq \frac{1}{(n+1)^3}\}$.
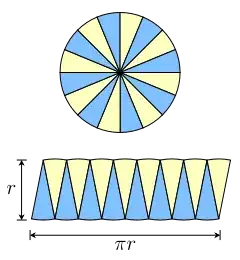
Still we may use this naive notion of area to compute the area of the unit circle. By considering the regular polygons in $\mathcal{I}$ and $\mathcal{E}$ we have
$$ \mu\left(\{(x,y):x^2+y^2\leq 1\right) = \sup_{n\geq 3}n\cdot\sin\frac{\pi}{n} = \inf_{n\geq 3}n\cdot\tan\frac{\pi}{n}=\pi $$
hence the area of the unit circle is just half the length of its boundary and $\pi\in(3,4)$ follows from the fact that
If $A,B$ are two convex, bounded sets in $\mathbb{R}^2$ and $A\subsetneq B$, the length of $\partial A$ is less than the length of $\partial B$. (see also this question)
An Archimedean-like geometric approach for the numerical approximation of $\pi$ is the following: a circle with radius $1$ can be decomposed as the union of an octagon with side length $\sqrt{2-\sqrt{2}}$ and eight circular segments. Such segments can be approximated by parabolic segments, whose area is simply $\frac{2}{3}\text{base}\cdot\text{height}$. The parabolic segments are slightly smaller than the corresponding circle segments, hence the following construction
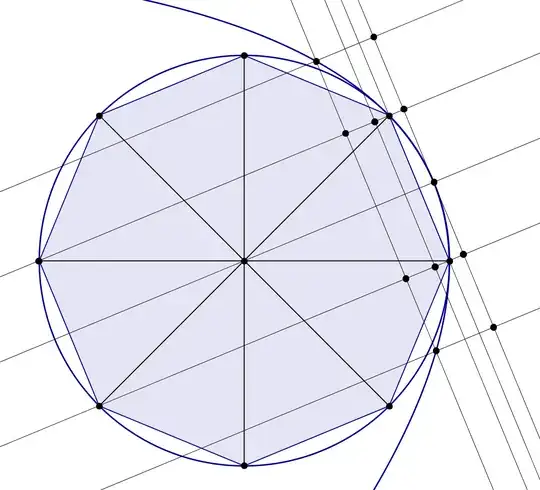
leads to the lower bound
$$\pi > \frac{16}{3}\sqrt{2-\sqrt{2}}-\frac{2}{3}\sqrt{2}= 3.13914757\ldots$$
whose accuracy is comparable with the actual Archimedean approximation $\pi\leq\frac{22}{7}$. The parabolic method applied to the regular dodecagon leads to the nice bound
$$ \pi > 4\sqrt{6}-4\sqrt{2}-1 = 3.1411\ldots $$
which also explains the proximity between $\pi$ and $\sqrt{2}+\sqrt{3}$.
A broader notion of area comes from defining the Riemann/Lebesgue integral and defining the area of $K\subset\mathbb{R}^2$ as
$$ \mu(K) = \iint_{\mathbb{R}^2}\mathbb{1}_K(x,y)\,dx\,dy $$
provided that the RHS makes sense. 1,2,3 are fulfilled, and this also allows us to measure the previous troubling sets. Additionally, this gives us new ways for approximating
$$\pi=4\int_{0}^{1}\sqrt{1-x^2}\,dx = 6\arcsin\frac{1}{2} = 3\sum_{n\geq 0}\frac{\binom{2n}{n}}{16^n(2n+1)}=3+\frac{1}{8}+\frac{9}{640}+\left(0\leq\varepsilon\leq 3\cdot 10^{-3}\right) $$
also through
$$ \frac{1}{5\cdot 4^8}\approx\int_{0}^{1}\frac{x^8(1-x)^8}{1+x^2}\,dx=4\pi-\frac{188684}{15015}.$$
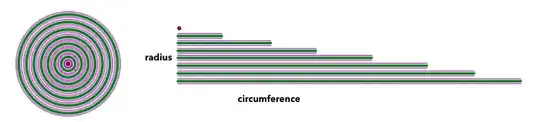
Improving the answer: why is it enough to study the unit circle? Because a circle is highly symmetric, os by applying a dilation with factor $\lambda>0$ the area is multiplied by $\lambda^2$ and the length of the boundary is multiplied by $\lambda$ (the fundamental property of affine maps is that they preserve the ratio of areas). In particular if the area of the unit circle is $\beth$, the area of a circle with radius $R$ is $\beth R^2$.
How is this related with the length of the boundary? Through convexity. If we consider the annulus between two concentric circles with radii $R$ and $R+\varepsilon$, the area of the annulus divided by $\varepsilon$ tends to the length of the boundary of the inner circle as $\varepsilon\to 0^+$. In particular if $\beth R^2$ is the area of the circle with radius $R$, the length of its boundary is given by
$$ \frac{d}{dR}\beth R^2 = \color{red}{2\beth}R.$$