How can we prove that $\pi > 3$ using this definition

Question

I've been trying to prove that $\pi > 3$ by using the following definition:

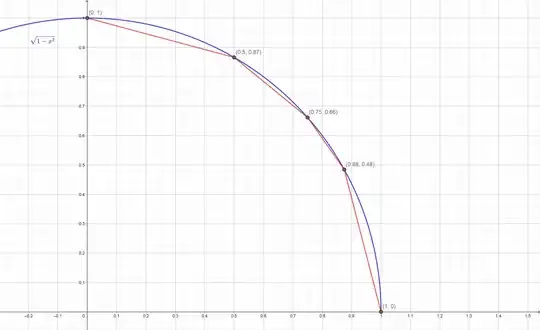
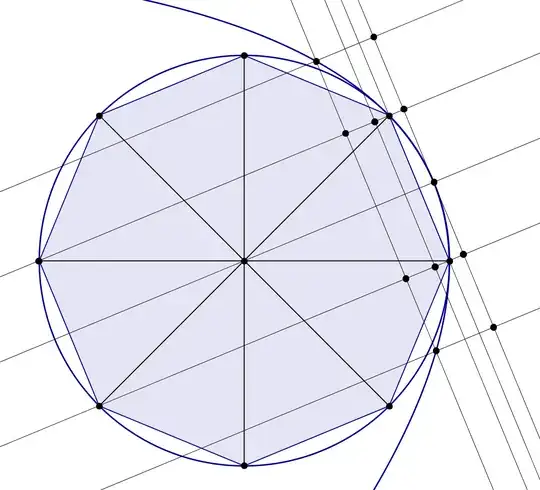
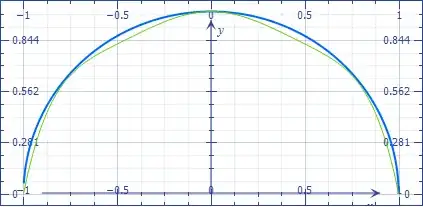
$$\pi = 2\int_{-1}^1{ {\sqrt{1-t^2}}}\, dt$$

Which comes from finding what the area of the unit circle is. (This path can be found in Spivak's Calculus, in case someone wants to read about this topic)

I've done it already using sums and geometry, but I'm having a really bad time trying to find a good starting point, let alone the entire path for this proof.

Any help would be greatly appreciated.

Answer 1

Let $f(t) = \sqrt{1-t^2}$. Since $f$ is even $$ 2 \int_{-1}^{1} f(t)\,dt = 4 \int_{0}^{1} f(t)\,dt $$

Bound $f$ from below with easily integrable functions, like straight lines. For example, in this case, the concatenation of the line segments connecting in order the points $(0, f(0))$, $\left(\frac{1}{2}, f(\frac{1}{2})\right)$, $\left(\frac{1}{2} + \frac{1}{4}, f(\frac{1}{2} + \frac{1}{4})\right)$, $\left(\frac{1}{2} + \frac{1}{4} + \frac{1}{8}, f(\frac{1}{2} + \frac{1}{4} + \frac{1}{8})\right)$ and $(1, f(1))$ is sufficient.

Let $L(t)$ the concatenation of these lines. Show that $3 < 4 \int_{0}^{1} L(t)\,dt$ and $L(t) \le f(t)$ for $t \in [0,1]$. Then conclude by the integral monotonicity that $$ 3 < 4 \int_{0}^{1} L(t)\,dt \le 4 \int_{0}^{1} f(t)\,dt $$

Actually you can partition the interval the way you prefer and with enough line segments you will be able to conclude the same.

Answer 2

The definition $\pi=2\int_{-1}^{1}\sqrt{1-x^2}\,dx$ is actually equivalent to $\pi=\Gamma\left(\frac{1}{2}\right)^2$, or to $\pi=2\arcsin(1)$, or to $\pi=6\arcsin\frac{1}{2}$, or to $$ \pi = \sum_{n\geq 0}\frac{3\binom{2n}{n}}{16^n(2n+1)}=\color{red}{3}+\frac{1}{8}+\frac{9}{640}+\frac{15}{7168}+\ldots $$ hence $\pi>3$ or even $\pi>\frac{25}{8}$ is just a consequence of the structure of the Maclaurin series of $\frac{1}{\sqrt{1-x^2}}$ and $\arcsin(x)$. This essentially is Newton's historical approach to the computation of $\pi$, rapidly superseded by Machin's identity $\pi=16\arctan\frac{1}{5}-4\arctan\frac{1}{239}$. Since $\pi=4\int_{0}^{1}\frac{dt}{1+t^2}$ and

$$ \int_{0}^{1}\frac{t^4(1-t)^4}{1+t^2}\,dt = \frac{22}{7}-4\int_{0}^{1}\frac{dt}{1+t^2} $$ we also have $\pi<3+\frac{1}{7}$ (this is the Archimedean approximation).
An Archimedean-like geometric approach is the following: a circle with radius $1$ can be decomposed as the union of an octagon with side length $\sqrt{2-\sqrt{2}}$ and eight circular segments. Such segments can be approximated by parabolic segments, whose area is simply $\frac{2}{3}\text{base}\cdot\text{height}$. The parabolic segments are slightly smaller than the corresponding circle segments, hence the following construction

leads to the lower bound $$\pi > \frac{16}{3}\sqrt{2-\sqrt{2}}-\frac{2}{3}\sqrt{2}= 3.13914757\ldots$$ whose accuracy is comparable with the actual Archimedean approximation. In such context $\pi>3$ simply follows from the fact that the area of a regular dodecagon inscribed in the unit circle is $3$.
The parabolic method applied to the regular dodecagon leads to the nice bound $$ \pi > 4\sqrt{6}-4\sqrt{2}-1 = 3.1411\ldots $$ which also explains the proximity between $\pi$ and $\sqrt{2}+\sqrt{3}$.
Back to sneaky tricks involving hypergeometric series, $$ \sum_{n\geq 1}\frac{1}{n^2(n+1)^2}=\frac{\pi^2-9}{3},\qquad \sum_{n\geq 1}\frac{1}{n^3(n+1)^3}=10-\pi^2 $$ clearly prove that $3<\pi<\sqrt{10}$, or that $\sqrt{78}<2\pi\sqrt{2}<\sqrt{79}$.

Answer 3

In the OP $\pi$ is defined as the area of the unit circle, and it is thus larger than the area of any inscribed, in the unit circle, canonical polygon.

We shall show that the area $A_{12}$ of the canonical 12-gon, inscribed in the unit circle is EXACTLY 3, and hence $\pi>3$.

Indeed, $$ A_{12}=12\times T_{12} $$ where $T_{12}$ is the area of the isosceles triangle with sides $1$, $1$ and $2\sin (\pi/12)$. In this triangle: $$ \mathrm{Height}=\cos(\pi/12)=\frac{\sqrt{6}+\sqrt{2}}{4},\quad \mathrm{Basis}=2\sin(\pi/12)=2\cdot\frac{\sqrt{6}-\sqrt{2}}{2} $$

and hence $T_{12}=\frac{1}{4}$ and $A_{12}=3$, and consequently, $\pi>3$.

Answer 4

Hint:

It can be shown rigorously that

$$\sqrt{1-t^2}\ge 1-t^2+\frac{t^4(1-t^2)}{0.65}$$

and the integral of the polynomial is $\frac{412}{273}>\frac32$.

Answer 5

I presume the integral is: $$\pi = 2\int_{-1}^1{ \frac{1}{\sqrt{1-t^2}}}dt$$ Hint: use the standard integral: $$2\int_{-1}^1{ \frac{1}{\sqrt{1-t^2}}}dt=2 \bigg[\arcsin t \bigg]_{-1}^{1}= 2\bigg[ \ arcsin (1) - \arcsin(-1)\ \bigg]>3$$

Answer 6

$$\pi = 2\int_{-1}^1{ {\sqrt{1-t^2}}dt}$$ Use the hint:: $t=\cos u$ to obtain: $$\pi = 2\int{ {\sqrt{(1-\cos^2u}}) du} = -2\int \sin (u)\sin (u)du= -2\int \sin^2(u) du$$ Can you continue from here?

Answer 7

$$\pi = 2\int_{-1}^1{ {\sqrt{1-t^2}}}dt$$ is the area of the unit disk.We can consider the area of regular dodecagon inside the unit circle which is very easy to compute.

Answer 8

See Trapezoidal rule, e.g. at Wikipedia.

You can show the function to be integrated is concave, so any approximation of its graph with a polygonal chain gives you a lower bound of the integral. Try to split the integration interval into some three, four pieces and see what happens.