0

$\text{Determine the } LDL^t \text{factorization of the positive definite matrix} \\ A= \begin{bmatrix} 4 & -1 & 1 \\ -1 & 4.25 & 2.75 \\ 1 & 2.75 & 3.5 \\ \end{bmatrix}$

In order to solve this problem I used the $LDL^t$ algorithm from here LDL Factorization

$L = zeros(3,3), D= zeros(3,1) \\ i =1..n \\ d(1) = A(1,1) = 4 \\ \text{For j = i+1 = 2 to 3} \\ L(2,1) = \frac{A(2,1)}{d(1)} = -\frac{1}{4} \\ j =3, i =1 \\ L(3,1) = \frac{A(3,1)}{D(1)} = \frac{1}{4} \\ L(3,2) = \frac{A(3,2) = A(3,2)- \Sigma^{1}_{k=1} L(3,1)\cdot L(2,1)\cdot(D(1))}{D(2) } = \frac{(2.75- (1/4) (-1/4)(4))}{4} = \frac{3}{4}\\ D(2)= A(2,2)- \Sigma^1_{j=1}L(2,1)^2(D(1)) =4.25-((-1/4)^2(4)= 4\\ D(3) = A(3,3) - (L(3,1)^2 \cdot D(1) + L(3,2)^2 \cdot D(2))= 3.5- ((1/4)^2(4))+ (3/4)^2(4) = 1 \\ \text{Lower Triangular }= \begin{bmatrix} 1 & 0 & 0 \\ -\frac{1}{4} & 1 & 0 \\ \frac{1}{4} &\frac{3}{4} & 1 \\ \end{bmatrix} , \text{Upper Triangular} =\begin{bmatrix} 4 & -1 & 1 \\ 0 & 4.0& 3.0\\ 0 & 0 & 1.0\\ \end{bmatrix} \\ \text{ and we have } A= LDL^T \\ \begin{bmatrix} 4 & -1 & 1 \\ -1 & 4.25 & 2.75 \\ 1 & 2.75 & 3.5 \\ \end{bmatrix} = \begin{bmatrix} 1 & 0 & 0 \\ -\frac{1}{4} & 1 & 0 \\ \frac{1}{4} &\frac{3}{4} & 1 \\ \end{bmatrix} \begin{bmatrix} 4 & 0 & 0 \\ 0 & 4 & 0 \\ 0 &0 & 1 \\ \end{bmatrix} \begin{bmatrix} 1 & -\frac{1}{4} & \frac{1}{4} \\ 0 & 1 &\frac{3}{4} \\ 0 &0 & 1 \\ \end{bmatrix} \\ $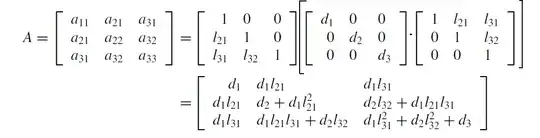enter image description here

Did I make any mistakes with the algorithm that solved the problem? The only mistake I might have made is when to increment the i in the nested loop.

Rodrigo de Azevedo
  • 1
Jon
  • 1,920

1 Answers1

0

I multiplied by 4 to get all integers in the original. The algorithm here is not guaranteed to give upper and lower triangular. However, it came out the same as yours, which would happen in the most favorable case.

I discuss the algorithm http://math.stackexchange.com/questions/1388421/reference-for-linear-algebra-books-that-teach-reverse-hermite-method-for-symmetr ..... I think there is a pretty good chance that the output will agree with your LDL when the original matrix is symmetric positive definite. Indeed, by Sylvester's Law of Inertia, one of the uses of solving $P^T HP = D$ (such that $D$ becomes diagonal) is to find out, without guesswork or approximation, how many eigenvalues of $H$ are positive, how many negative, and how many exactly zero.

$$ P^T H P = D $$ $$\left( \begin{array}{rrr} 1 & 0 & 0 \\ \frac{ 1 }{ 4 } & 1 & 0 \\ - \frac{ 7 }{ 16 } & - \frac{ 3 }{ 4 } & 1 \\ \end{array} \right) \left( \begin{array}{rrr} 16 & - 4 & 4 \\ - 4 & 17 & 11 \\ 4 & 11 & 14 \\ \end{array} \right) \left( \begin{array}{rrr} 1 & \frac{ 1 }{ 4 } & - \frac{ 7 }{ 16 } \\ 0 & 1 & - \frac{ 3 }{ 4 } \\ 0 & 0 & 1 \\ \end{array} \right) = \left( \begin{array}{rrr} 16 & 0 & 0 \\ 0 & 16 & 0 \\ 0 & 0 & 4 \\ \end{array} \right) $$ $$ Q^T D Q = H $$ $$\left( \begin{array}{rrr} 1 & 0 & 0 \\ - \frac{ 1 }{ 4 } & 1 & 0 \\ \frac{ 1 }{ 4 } & \frac{ 3 }{ 4 } & 1 \\ \end{array} \right) \left( \begin{array}{rrr} 16 & 0 & 0 \\ 0 & 16 & 0 \\ 0 & 0 & 4 \\ \end{array} \right) \left( \begin{array}{rrr} 1 & - \frac{ 1 }{ 4 } & \frac{ 1 }{ 4 } \\ 0 & 1 & \frac{ 3 }{ 4 } \\ 0 & 0 & 1 \\ \end{array} \right) = \left( \begin{array}{rrr} 16 & - 4 & 4 \\ - 4 & 17 & 11 \\ 4 & 11 & 14 \\ \end{array} \right) $$

Will Jagy
  • 139,541