5

It is well-known that gaps between successive primes have i.e. multimodal distribution (with peaks at $6 k$):

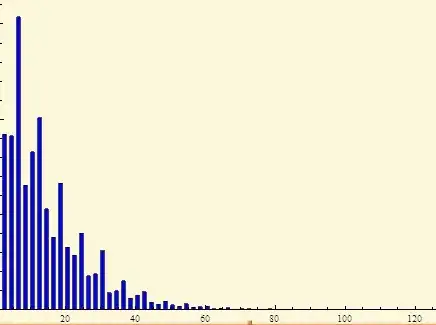
Prime gaps histogram

I'm interested to know: what is the most suitable approximation for such weird distributions? The envelope of peaks looks like $\chi^2$ ??

Community
  • 1
lesobrod
  • 774
  • See http://math.stackexchange.com/questions/106417/what-is-prime-gaps-relationship-with-number-6?rq=1 – Yury Dec 31 '12 at 15:57

2 Answers2

4

Asymptotically it depends on the radical of k: basically take $$ f(k)=\prod_{p|k,\ p>2}\frac{p-1}{p-2} $$ and compare for different k. So f(6) = 2 > 1 = f(8), so gaps of length 6 are asymptotically twice as common as gaps of length 8. (Obviously k needs to be even.)

You asked (in a comment) for a smooth envelope. Using Mertens' theorem and the Prime Number Theorem it can be shown that $$ f(k)=O(\log\log k) $$ and this bound is tight in the sense that there is some $\alpha$ with $f(k)>\alpha\log\log k$ for infinitely many $k$. (This can be computed without too much difficulty, if desired.)

You might notice that this does not resemble the curve you have drawn. This is the result of a number of separate factors:

  1. The envelope necessarily ignores low points, so only 2, 6, 30, ... are relevant.
  2. There is a discretization error such that the small members do not fit the curve very nicely. It works better for large k, say $k\ge 2\cdot3\cdot5\cdot7$. The error diminishes approximately as $O(1/\log\log k)$.
  3. Your graph uses a small number of prime gaps. This error decreases approximately as $O(k/\log x)$ where x is the number of prime gaps used. In particular, every time you double k you need to square the number of prime gaps used to keep the error roughly constant.
Charles
  • 32,122
  • OK but what about some smooth multi-peaks envelope? – lesobrod Dec 31 '12 at 16:45
  • @lesobrod: You can get a smooth envelope with Mertens' theorem and the Prime Number Theorem, but it won't look like your graph because it looks at large numbers where yours is influenced greatly by small numbers. I'll edit the answer. – Charles Jan 01 '13 at 19:42
-1

EMPIRICAL RESULTS:

We are talking about primes in some interval between xbar-dx to xbar+dx where xbar is up to around 10^40, and dx is up to around sqrt(xbar)

The number of gaps G between successive primes p = 6*k+1 in this interval can be approximated by a log-linear distribution: log( G(6*k) ) = A + B*k, for k = 1, 2, ... N small enough.

Similarly, The number of gaps G between successive primes p = 6*k-1 in this interval can be approximated by a log-linear distribution: log( G(6*k) ) = C + D*k, for k = 1, 2, ... N small enough.

The results for (6*k+1) and (6*k-1) need to be combined to get the approximation for gaps between all the primes.

Arnold Soltz
  • 1