Algebraic closure of the $p$-adic integers

Question

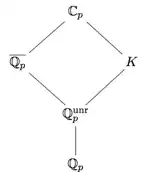
Let $p$ be a prime number.

• 1. What is the degree over $\Bbb Q_p$ of 'the' algebraic closure $\overline{\Bbb Q_p}$ of $\Bbb Q_p$ ?
• 2. What is the order (the cardinality) of the absolute Galois group $G$ of $\Bbb Q_p$ ?
• 3. What is the degree over $\overline{\Bbb Q_p}$ of the completion $\Bbb C_p$ of $\overline{\Bbb Q_p}$ ?

$ $

---

Here are some comments and thoughts :

1)

I know that $[\overline{\Bbb Q_p} : \Bbb Q_p] \geq \aleph_0$, since $X^n-p$ is irreducible in the UFD $\Bbb Z_p[X]$ for any $n \geq 1$. According to an answer here, we have $[\overline{\Bbb Q_p} : \Bbb Q_p] = \aleph_0$, but there is no proof of this claim.

Since $\Bbb Q_p$ has a unique unramified extension of degree $n$ for any $n \geq 1$, we have $[\Bbb Q_p^{\rm unr} : \Bbb Q_p] = \aleph_0$.

In general, we have $|k| =|k^{\rm sep}| = |\bar k|$, when $k$ is infinite (see here, exercise 4.5). But it doesn't help for knowing $[\bar k : k]$ (nor $[k^{\rm sep} : k]$, think of the separably closed but not algebraically closed field $\Bbb F_p(T)^{\rm sep}$). As mentioned here, we can have fields $k$ with $[\bar k : k] > \aleph_0$. In general, I think that we have $[\bar k : k] \leq |k|$ when $k$ is infinite. For any infinite field $k$ and any set $I$, we have $|k^{(I)}| = |k| \cdot |I| = \max(|k|, |I|)$ (where $\dim_k(k^{(I)}) = |I|$, while $\dim_k(k^{I}) = |k^I| = |k|^{|I|}$).

2)

Since $G$ surjects onto the absolute Galois group $\widehat{\Bbb Z}$ of $\Bbb F_p$, it is uncountable — I don't know if one can use a similar proof as for the absolute Galois group of $\Bbb Q$, using permutation of the square roots of primes, using this (maybe the fact that $\Bbb Q_p^{\times, 2}$ has finite index in $\Bbb Q_p^{\times}$ [$8$ if $p=2$ and $4$ if $p>2$] could be a problem?).

Moreover, $G$ is at most of cardinality $|\mathrm{Bij}(\overline{\Bbb Q_p})| = 2^{2^{\aleph_0}}$. So how to choose (assuming GCH...) between $2^{\aleph_0}$ and $2^{2^{\aleph_0}}$ for the cardinality of $G$ ?

3)

My question here asked about the degree of $\Bbb C_p$ over a completion of some subfield of $\overline{\Bbb Q_p}$, which is different from here. I know that $[\Bbb C_p : \overline{\Bbb Q_p}]>1$, but it is not obvious to me that this degree is $\geq \aleph_0$. (By the way, we have $|\Bbb C_p| = 2^{\aleph_0}$ by exercise 2.30.5 here).

According to Arithmetic of Algebraic Curves (Stepanov), p. 239(d), the transcendence degree of $\Bbb C_p$ over $\overline{\Bbb Q_p}$ is already $2^{\aleph_0}$, without proof. I'm not sure how to prove this, and actually I should think to the relation between $\mathrm{tr.deg}_k(L)$ and $[L:k]$ : if $B$ is a transcendence basis of $L$ over an infinite field $k$, then we have $$|k| \cdot |B| = [k(B) : k] \leq [L:k] \leq [\overline{k(B)} : k] \leq |k| \cdot |B| \cdot |k(B)| = (|k| \cdot |B| ) \cdot (|k| \cdot |B|)$$ In particular, if $|B| = \mathrm{deg.tr}_k(L) = 2^{\aleph_0} = |k|$, then we get $[L:k] = 2^{\aleph_0}$ (see also 11.4 here...).

Thank you for your various comments!

Answer 1

$\newcommand{\Q}{\Bbb Q} \newcommand{\trdeg}{\mathrm{tr.deg}} \newcommand{\C}{\Bbb C} \newcommand{\unr}{\rm unr}$ Thanks to Prof. Lubin's comment above and thanks to some fortunate searches, I can provide an answer.

1) From Proposition 14, II, §5 of Lang's Algebraic number theory, we know that, for any $n \geq 1$, the field $\Q_p$ has only finitely many extensions of degree $n$. It follows that the degree of $\overline{\Q_p}$ over $\Q_p$ is $\aleph_0$.

2) As $G$ is an inverse limit of the finite groups $\mathrm{Gal}(K / \Q_p)$, where $K$ runs over the countable set of finite Galois extensions of $\Q_p$, we see that $G$ has cardinality at most $2^{\aleph_0}$, hence exactly $2^{\aleph_0}$ (see the thoughts to my question above).

3) This is more difficult. The answer is given as theorem 3 in the paper David Lampert, Algebraic $p$-adic expansions, Journal of Number Theory, volume 23 (3), 1986, pp. 279-284. Consider the tower of extensions, where $K = \widehat{ \Q_p^{\unr} }$ :

$\hspace{6cm}$

We have, according to the cited paper : $$\trdeg_{\Q_p}(K) = \trdeg_K(\C_p) = 2^{\aleph_0}.$$

Then, by additivity of the transcendence degree, we have $$\trdeg_{\Q_p^{\unr}}(\C_p) = \trdeg_{\Q_p^{\unr}}( \overline{\Q_p} ) + \trdeg_{\overline{\Q_p}}(\C_p) = \trdeg_{\Q_p^{\unr}}(K) + \trdeg_K(\C_p) = \trdeg_{\Q_p}(K) - \trdeg_{\Q_p}(\Q_p^{\unr}) + \trdeg_K(\C_p),$$ which boils down to $$\trdeg_{\Q_p^{\unr}}(\C_p) = \trdeg_{\overline{\Q_p}}(\C_p) = 2^{\aleph_0} - 0 + 2^{\aleph_0} = 2^{\aleph_0}.$$ Since $\#\C_p = \#\overline{\Q_p} = 2^{\aleph_0},$ it is easy to conclude that $[\C_p : \overline{\Q_p}] = 2^{\aleph_0}$.