4

$\newcommand{\Q}{\mathbb{Q}} \DeclareMathOperator{\unr}{unr} \newcommand{\C}{\mathbb{C}} $

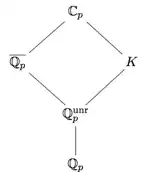
Denote by $\Q_p^{\unr}$ the maximal unramified extension of the field of $p$-adic numbers $\Q_p$ (where $p$ is any prime). The $p$-adic absolute value on $\Q_p$ has a unique extension to $\Q_p^{\unr}$, which I denote $| \cdot |_p$.

I would like to know what is the completion $K$ of $\Q_p^{\unr}$ with respect to $| \cdot |_p$. It is known that $K \neq \Q_p^{\unr}$. I wonder if $K = \C_p$ holds, where $\C_p$ denotes the completion of the algebraic closure $\overline{\Q_p}$ of $\Q_p$, or equivalently the completion of $\overline{\Q}$ with respect to $| \cdot |_p$. So here is my precise question :

What is the degree $[\C_p : K]$ equal to ?

By Artin–Schreier's theorem and because $\C_p$ is algebraically closed, if $1 < [\C_p : K] < \infty$, then $K$ would be a real closed field, which is not the case because $K$ contains non-trivial roots of unity. Therefore, the degree $[\C_p : K]$ is either $1$ or is some infinite cardinal.

Any idea about my question will be appreciated.

Watson
  • 23,793
  • 4
    The degree is infinite: the roots of $x^n=p$ have degree $n$ over $K$. The real question is which infinite cardinal is $|\Bbb C_p:K|$? – Angina Seng Oct 07 '17 at 14:43
  • 1
    @LordSharktheUnknown : thank you for your comment. In that case, I would like to know which infinite cardinal the degree is. (I see that $X^n-p$ is irreducible over the valuation ring $O_K$ of $K$ by Eisenstein's criterion, hence over $K$ by Gauss' lemma). – Watson Oct 07 '17 at 14:49
  • [In my comment above, I'm precisely using the fact that $O_K$ is a DVR (hence PID, UFD, …), since $K$ is the completion of an unramified extension of $\Q_p$]. – Watson Oct 07 '17 at 15:00
  • 2
    @LordSharktheUnknown has put his finger on the real question. Since $\Bbb C_p$ itself is still of only continuum cardinality, the field extension degree can only be countable infinite or continuum (granting CH of course). I spent a handful of minutes trying to show uncountability of the degree, which seems the only plausible answer, but got nowhere. Maybe someone else can illuminate. – Lubin Oct 09 '17 at 02:47
  • By the way, the completion of the maximal unramified extension of a local field appears naturally in local class field theory, e.g. see §2.2 in Local Class Field Theory Is Easy by MICHIEL HAZEWINKEL. – Watson Oct 11 '17 at 19:47
  • (Also see III.§4, p. 47, in Neukirch's Class Field Theory). – Watson Oct 23 '17 at 15:38
  • 1
    Also see https://mathoverflow.net/questions/85204/ring-of-witt-vectors-and-p-adics: the completion $K$ of $\mathbf Q_p^{\text{unr}}$ is the fraction field of the Witt vectors of $\overline{\mathbf F_p}$. In particular, the ring of integers (unit disc) of $K$ is a DVR with prime element $p$, which is very far from being the ring of integers of $\mathbf C_p$. This doesn't directly answer the question, but I wanted to point out that you can see for algebraic reasons that $K$ is definitely not $\mathbf C_p$. – KCd Jan 13 '20 at 06:50

2 Answers2

3

$\newcommand{\Q}{\Bbb Q} \newcommand{\trdeg}{\mathrm{tr.deg}} \newcommand{\C}{\Bbb C} \newcommand{\unr}{\rm unr}$

The answer is given as theorem 3 in the paper David Lampert, Algebraic $p$-adic expansions, Journal of Number Theory, volume 23 (3), 1986, pp. 279-284. Consider the tower of extensions, where $K = \widehat{ \Q_p^{\unr} }$ :

$\hspace{6cm}$

We have, according to the cited paper : $$\trdeg_{\Q_p}(K) = \trdeg_K(\C_p) = 2^{\aleph_0}.$$ Since $\#\C_p = \#\Q_p = \# K = 2^{\aleph_0},$ it is easy to conclude that $[\C_p : K] = 2^{\aleph_0}$ (this is the algebraic degree – no Hilbert basis or whatever).

Watson
  • 23,793
1

Let me try to answer to the question - as modified by @Lubin - not in terms of "infinite degrees" (perhaps too vague a notion) but in terms of cardinals of Galois groups. As a base field, take an ultrametric complete field $K$, say a finite extension of $\mathbf Q_p$ for simplification, and an algebraic closure $\bar K$ with Galois group $G_K=Gal(\bar K/K)$ and completion $\hat {\bar K}$. It is known that any automorphism in $G_K$ acts as an isometry hence its action can be extended to $\hat {\bar K}$ by continuity. For a closed subgroup $H$ of $G_K$, let $L$ be the fixed field of $H$, so that $H=G_L=Gal(\bar K /L)$ . In the OP question, $K=\mathbf Q_p$ and $L=\mathbf Q_p^{nr}$.

A central result in this context is the Ax-Sen-Tate theorem (*), which states states that $\hat {L}=(\hat {\bar K})^H$, so in particular $H=Gal(\hat {\bar K}/\hat {L})$. Take $L= K^{nr}$, so $H=G_{K^{nr}}$. Replacing the "degree" of $\hat {\bar K}/\hat {L}$ by card $H$, we want to show that $H$ is not enumerable. The advantage of the AST theorem is to bring us back to "usual" algebraic extensions (not necessarily complete). The algebraic closure $\bar K$ contains the maximal abelian extension $K^{ab}$ of $K$, and so $G_{K^{nr}}$ surjects onto $Gal(K^{ab}/K^{nr})$, which is known by local CFT to surject onto $\mathbf Z_p$, see e.g. Cassels-Fröhlich, chap.VI, §2.8 (in the case $K=\mathbf Q_p$, this is just the local Kronecher-Weber theorem, op. cit. §3.1). But card $\mathbf Z_p=\aleph_1$, and we are done .

(*) J. Tate, "$p$-divisible groups", Proc. Conf. Local Fields, 1966

nguyen quang do
  • 14,578
  • 2
    But, but, but… The equality of field extension degree with the cardinality of the Galois group is valid only for finite extensions. The field extension degree may well be countable while the Galois group is of uncountable cardinality. Indeed, infinite Galois groups are profinite, which guarantees uncountability. But the example of $\overline{\Bbb Q}\supset\Bbb Q$ (the algebraic closure, that was) shows that the dimension may be countable. – Lubin Oct 10 '17 at 22:17
  • 1
    True, but I said as a preliminary that I would shift to Galois groups because "infinite degree" makes me uneasy. The natural definition would be $[L:K]$ = dimension of the $K$-vector space $L$, but what dimension ? In the algebraic sense, only finite $K$-linear combinations are allowed; in the topological sense (here, in a normed vector space), infinite convergent l.c. come into play. Mixing algebra and topology can give such results as : if $K$ is complete w.r.t. a non discrete valuation, no normed space of countable algebraic $K$-dimension can be complete (if I remember well). – nguyen quang do Oct 11 '17 at 07:10
  • I agree with your example of $\bar {\mathbf Q}/\mathbf Q$, but there is no topology in these fields, whereas the difficulty in the OP question seems to be about the dimension (algebraic or not) of a complete normed vector space w.r.t. a discrete valuation. On the Galois side, the gist of the AST theorem was to show that the problem could be brought back to a Galois extension with no topology involved in the fields. It's true that any profinite group is uncountable, and I should have stopped there. The problem of the cardinality of the degree (algebraic or topological) remains unsolved. – nguyen quang do Oct 11 '17 at 07:36
  • Hmm, interesting. So I guess you’re moving from what the analysts call Hamel bases to Banach-space bases. I think my mind is starting to melt. – Lubin Oct 11 '17 at 18:19
  • Mine too ! Actually I have no idea how to do this using the Galois group. – nguyen quang do Oct 11 '17 at 20:45
  • @nguyenquangdo : You might be interested by the answer I wrote. – Watson Mar 05 '18 at 18:36
  • @Watson, Yes, I've taken a look, thank you. – nguyen quang do Mar 08 '18 at 08:18