2

Assume that I have four points $P_1, P_2, P_3, P_4$. These points lie on the 2d plane and take the form $P_i = (x_i, y_i)$

Assume that I define line $L_{ij}$ as the line passing through $P_i$ and $P_j$.

How do I find the coefficients $a$ and $b$ in the equation for an ellipse $\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$ such that the ellipse passes through points $P_2$ and $P_3$ AND has both tangent lines $L_{12}$ and $L_{34}$?

EDIT: I am using this formula to smooth a graph I'm drawing in python's matplotlib.pyplot. I have two line segments $L_{12}$ and $L_{34}$ that I need to draw a smooth connection through, and an ellipse seems like a good shape for this.

Paul Terwilliger
  • 289
  • For a starter, I'd advise you to introduce the center coordinates of the ellipse as parameters, otherwise your problem is highly unlikely to have a solution (in general). Once you've done that, you can probably solve this by expressing your various conditions as equations and solve the resulting system. – N.Bach Feb 26 '18 at 19:02
  • Of course you can't have, in general, an ellipse with that equation: such an ellipse would have the $x$ and $y$ axes as symmetry axes, but that can't be the case for general positions of points $P_i$. – Intelligenti pauca Feb 27 '18 at 12:47

4 Answers4

3

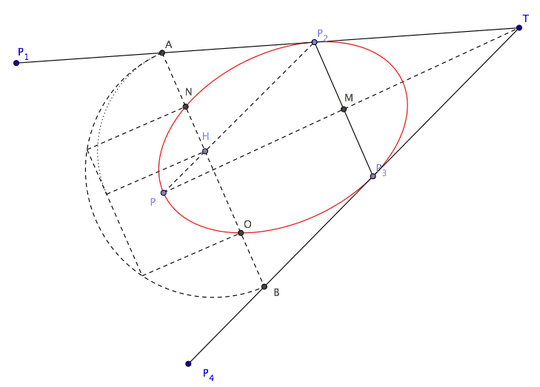
In a purely geometric fashion, given two tangents and two tangency points on them, enter image description here

the wanted ellipse can be constructed as the Steiner inellipse of $ABC$, where $A$ is given by the intersection of the given tangents and $B,C$ are given by the symmetric of $A$ with respect to the tangency points. In particular the center of the wanted ellipse lies at the centroid of $ABC$.

Jack D'Aurizio
  • 353,855
1

The slop of lines $L_{12}$ and $L_{34}$ are easily computed and we know that the slop of $L_{12}$ is the value of derivation $y\prime$ in $$\frac{x_2}{a^2}+\frac{y_2y'}{b^2}=0 $$ and similarly for the slope of $L_{34}$ the same argument holds, this time $y\prime$ being the slop of $L_{34}$.

There fore we have two linear equations with unknowns $a^2$ and $b^2$. This system of linear equations can easily be solved and also we may decide if any 4-tuple $(P_1,P_2,P_3,P_4)$ makes such ellipse.

Qurultay
  • 5,224
1

If you're after an ellipse that passes through 2 points with given tangents at those points then this may be of use to you[1].

[1] Roundest ellipse with specified tangents

fuzzy
  • 81
1

Here's a geometric construction for an ellipse tangent to lines $P_1P_2$, $P_3P_4$ at tangency points $P_2$, $P_3$. There is some freedom left in the construction, so you can fix another point on the ellipse, as explained below.

Let $T$ be the point where lines $P_1P_2$ and $P_3P_4$ meet. If $M$ is the midpoint of $P_2P_3$, ray $TM$ passes through the center of the ellipse and you can choose at will on it another point $P$ of the ellipse (provided $M$ lies between $T$ and $P$): every choice of $P$ will lead to a different ellipse satisfying your request. If you need, in particular, an ellipse of minimum eccentricity, you can choose $P$ as explained here.

To find other two points on the ellipse, take any point $H$ on $PP_2$ and draw through it a line parallel to $P_2P_3$, meeting line $P_1P_2$ at $A$ and line $P_3P_4$ at $B$. Construct then on segment $AB$ two points $N$ and $O$ such that $AN\cdot BN=AH^2$ and $BO=AN$ (a possible geometric construction is hinted in the diagram below). These two points also belong to the ellipse, which is then fully specified as the conic section passing through $P_2P_3OPN$.

enter image description here

In case lines $P_1P_2$ and $P_3P_4$ are parallel, construct line $MT$ through $M$ and parallel to them, then go on as explained above.

You should have no problems in working out the coordinates of $P$, $N$ and $O$. Once you have the five points, you can find the ellipse equation by substituting their coordinates in the generic equation $x^2+ay^2+bxy+cx+dy+e=0$ to find the unknown coefficients $a$, $b$, $c$, $d$, $e$.

Intelligenti pauca
  • 50,470
  • 4
  • 42
  • 77