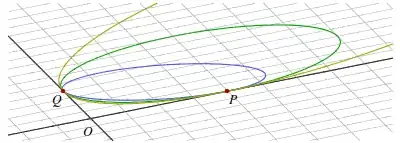
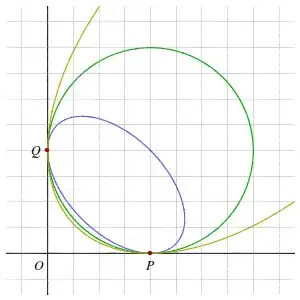
At the moment I can offer an analytical solution, which is quite cumbersome but manageable. I hope someone will be able to give a simpler solution.
To reduce the number of parameters, we can set up a coordinate system such that $\mathbf{p}_1=(\alpha,0)$, $\mathbf{p}_2=(0,\beta)$, $\mathbf{v}_1=(0,1)$, and define then $m=v_{2y}/v_{2x}$.
Let's start with the generic equation for a conic section, where we can set to $1$ the coefficient of $x^2$ because we are dealing with an ellipse:
$$
x^2+By^2+Cxy+Dx+Ey+F=0.
$$
We have four conditions: the conic passes through $\mathbf{p}_1$, $\mathbf{p}_2$ and is there tangent to $\mathbf{v}_1$, $\mathbf{v}_2$. These conditions translate into four equations:
$$
\begin{align}
\cases{
\alpha^2+\alpha D+F=0\\
\beta^2B+\beta E+F=0\\
2m\beta B+\beta C+D+mE=0\\
\alpha C+E=0
}
\end{align}
$$
From there, one can find expressions for $B$, $C$, $D$, $E$ as a function of $F$. Plugging these into the formulas for the semiaxes $a$ and $b$ we can then compute the eccentricity $\epsilon=\sqrt{1-b^2/a^2}$. The smaller the eccentricity, the rounder the ellipse, so we must find the minimum of $\epsilon$ as a function of $F$.
I computed $d\epsilon/dF$ with Mathematica and found that it vanishes for
$$
F=-\frac{\alpha ^2 \beta \left(\alpha ^2 \beta +\beta ^3-2 \alpha ^2 \beta m^2+2 \alpha ^3
m\right)}{\beta ^2 \left(\alpha ^2+\beta ^2\right)+2 m^2 \left(\alpha ^4+2 \alpha ^2 \beta
^2\right)+2 \alpha \beta m \left(\alpha ^2+2 \beta ^2\right)}.
$$
Once $F$ is known, one can compute the other coefficients and find the equation of the "roundest" ellipse:
$$
\begin{align}
\cases{
B=\frac{\displaystyle\alpha ^2 \left(\beta ^2+\alpha ^2 \left(2 m^2+1\right)+2 \alpha \beta m\right)}{\displaystyle\beta ^2\left(\alpha ^2+\beta ^2\right)+2 m^2 \left(\alpha ^4+2 \alpha ^2 \beta ^2\right)+2 \alpha
\beta m \left(\alpha ^2+2 \beta ^2\right)}\\
\\
C=\frac{\displaystyle2 \alpha ^2 m \left(-\alpha ^2+\beta ^2+2 \alpha \beta m\right)}{\displaystyle\beta ^2 \left(\alpha
^2+\beta ^2\right)+2 m^2 \left(\alpha ^4+2 \alpha ^2 \beta ^2\right)+2 \alpha \beta m
\left(\alpha ^2+2 \beta ^2\right)}\\
\\
D=-\frac{\displaystyle2 \alpha ^2 m \left(2 \beta ^3+m \left(\alpha ^3+3 \alpha \beta ^2\right)\right)}{\displaystyle\beta ^2
\left(\alpha ^2+\beta ^2\right)+2 m^2 \left(\alpha ^4+2 \alpha ^2 \beta ^2\right)+2 \alpha
\beta m \left(\alpha ^2+2 \beta ^2\right)}\\
\\
E=-\frac{\displaystyle2 \alpha ^3 m \left(-\alpha ^2+\beta ^2+2 \alpha \beta m\right)}{\displaystyle\beta ^2 \left(\alpha
^2+\beta ^2\right)+2 m^2 \left(\alpha ^4+2 \alpha ^2 \beta ^2\right)+2 \alpha \beta m
\left(\alpha ^2+2 \beta ^2\right)}
}
\end{align}
$$
A check with GeoGebra confirms that this is indeed the value of $F$ giving a minimum eccentricity.
EDIT.
Following the suggestion by Rahul, we can get a much simpler result. Choose a coordinate system such that
$\mathbf{p}_1=(\alpha,0)$, $\mathbf{p}_2=(-\alpha,0)$,
and define $m=v_{1y}/v_{1x}$, $n=v_{2y}/v_{2x}$.
With those choices, the equation of the ellipse can be written as:
$$
x^2+By^2-{m+n\over mn}xy+\alpha{m-n\over mn}y-\alpha^2=0.
$$
The eccentricity $\epsilon$ is then a function of $B$, and
$d\epsilon/dB=0$ for
$$
B=1+\frac{(m+n)^2}{2 m^2 n^2}.
$$
In summary, the equation of the roundest ellipse turns out to be:
$$
x^2+\left(1+\frac{(m+n)^2}{2 m^2 n^2}\right)y^2-{m+n\over mn}xy+\alpha{m-n\over mn}y-\alpha^2=0.
$$
Added by Rahul:
Things become even simpler if we use the slope of the normals, $\mu=-1/m$ and $\nu=-1/n$:
$$
x^2+\left(1+\tfrac12(\mu+\nu)^2\right)y^2+(\mu+\nu)xy+\alpha(\mu-\nu)y-\alpha^2=0.
$$