Proving that this is true for all x in the sequence.

Question

TL;DR -

Is it true, and how should I prove that for all $t$ that can be expressed as $u^2+uv-v^2$ for some $u, v \in \Bbb{Z}$, $$\frac{x^2+xy+y^2}{xy-t} = 4$$ has a pair of solution $(x, y) \in \Bbb{N}^2$?

After reading this post, I have tried to generalize the question by replacing the $1$ in the denominator by $t$, i.e. on

$$\frac{x^2+xy+y^2}{xy-t} = c.$$

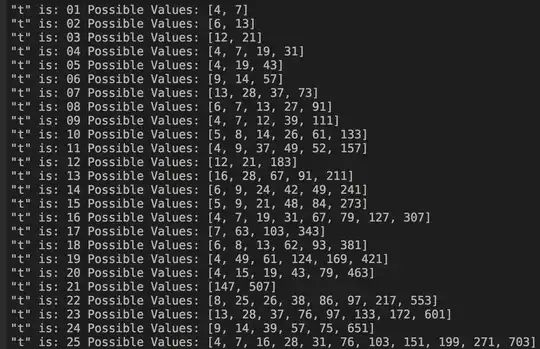
I focused on the different possible non-negative integer values for $c$ (for $x, y$ $\in$ $\Bbb{N}$). Then I run a 'tiny' computer search. Here's the result:

I observed that there is a lot of $4$s in the arrays, so I filtered them out:

So here is my result: when t is in the list below, $4$ is a possible value of $c$: [1, 4, 5, 9, 11, 16, 19, 20, 25, 29, 31, 36, 41, 44, 45, 49, 55, 59, 61, 64, 71, 76, 79, 80, 81, 89, 95, 99]

Doing a simple OEIS search gives us the sequence A031363.

And checking for all values in the OEIS sequence up to 10k, they all give $4$ as a possible value for $c$.

So here is my question after all the nonsense story:

Is it true, and how should I prove that for all $t$ that can be expressed as $u^2+uv-v^2$ for some $u, v \in \Bbb{Z}$, $$\frac{x^2+xy+y^2}{xy-t} = 4$$ has a pair of solution $(x, y) \in \Bbb{N}^2$?

(This is actually not proven to be true, so I am here to conjecture this.)

Thanks for reading, any tips or hints would be greatly appreciated!

Related: Number written in both forms (Also by me)

Answer 1

For any $t \in \mathbb{N}_+$ such that$$ t = u^2 - v^2 + uv $$ for some $u, v \in \mathbb{N}$, note that $u$ and $v$ cannot be $0$ simultaneously, then take$$ (x, y) = (2u + 2v, 2u), $$ and$$ \frac{x^2 + xy + y^2}{xy - t} = \frac{12u^2 + 4v^2 + 12uv}{4u^2 + 4uv - t} = 4. $$

Answer 2

The direction you ask about at the end is straightforward. $$ x^2 + xy + y^2 = 4xy - 4 t \; , $$ $$ x^2 - 3 x y + y^2 = -4 t. $$ The quadratic form $x^2 - 3 xy + y^2$ has discriminant $ 9 - 4 = 5.$ This means it is integrally equivalent to the other for you ask about, as $h(5) = 1.$ Indeed, if we take the (integer invertible) change of variables $$ x = p + 2 q \; , \; \; y = q \; , $$ $$ x^2 - 3 xy + y^2 = p^2 + pq - q^2. $$ Next, with $p^2 + pq - q^2 = -4 t,$ we cannot get an even number unless both $p,q$ are even. Let $r=p/2, \; \; s = q/2, \;$ we get $$ r^2 + rs - s^2 = -t. $$ We can also multiply by $-1$ easily enough. We take $u = s, \; v = r+s, \;$ we get $$ u^2 + uv - v^2 = t \; . $$