EDITED: Q11 is answered.
Please have a look at this origin post: Dog bone-shaped curve
In case not to make the question too long and make it horrific, I decided to open a new post for $2$ new subquestions,
11)(Answered, see comment by Yuriy S) Find the area (maybe not 'integral', since in definition to Riemann-integral, integral under x-axis is negative, but clearly area can't be negative) of the shaded green region and (*or) blue region, see the image below and here: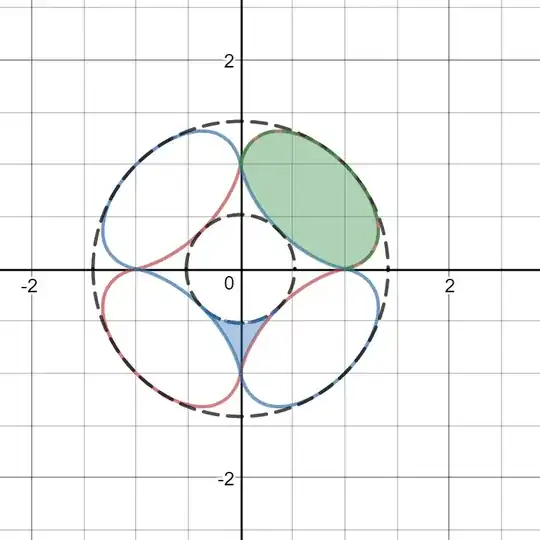
The area of the dog bone, which is the region enclosed by curve $f$, is already integrated by Barry Cipra in the answer of the origin post, which gave a result $A≈3.52723$.
*Therefore, by the areas of circle and dog bone, I believe it is easy (Using simple $+,-,\times,\div$) to find the area of one of the $2$ regions whenever knowing the another region's area.
I believe one need to change the curve into functions to find the area, see the answers to the origin post, especially those by Barry Cipra and Yuriy S.
By the way, I think the description of the green shaded area is quite interesting, as is invented by myself:
$$\bigl(\left|x\cos a-y\sin a\right|^{x\cos a-y\sin a}>\left|x\sin a+y\cos a\right|^{x\sin a+y\cos a}\bigr)$$
$$\land\bigl(x\cdot\cos a-y\sin a<x\sin a+y\cos a\bigr)$$
$$\land\Biggl(\max\Bigl(\min(|x|^x-|y\|^y,-x+y),\min(-|x|^x+|y|^y,x-y)\Bigr)<0\Biggr)$$
(In this situation, $a=\frac{\pi}{2}$)
12) It will be fun if anyone can integrate both green and blue area in terms of $a$, while $a$ is the rotation degree (clockwise) of the red dog bone! (See the description of the green shaded area above)
See the image and here: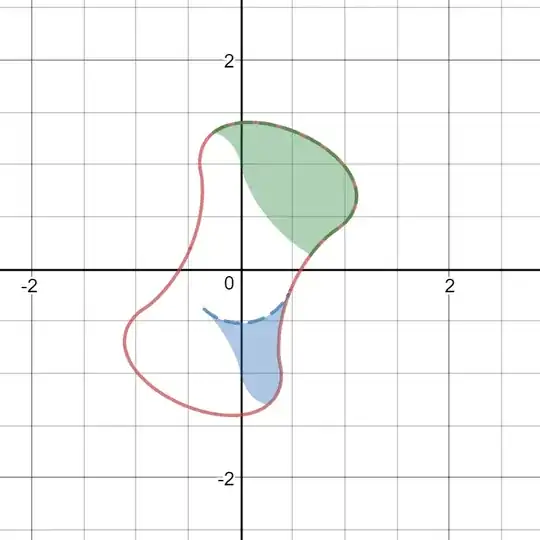 What I discover so far, are, the area of the green region be $\lt \frac{A}{2}≈1.76$, while the area of the blue region should be $\lt\frac{A}{2}-\frac{\pi(\frac{2}{\sqrt e})^2}{2}\approx 1.338$ (As the radius of inscribed circle $=\frac{2}{\sqrt e}$), no matter what $a$ is :). Any help, such as verification of my discoveries right above, will be appreciate :).
What I discover so far, are, the area of the green region be $\lt \frac{A}{2}≈1.76$, while the area of the blue region should be $\lt\frac{A}{2}-\frac{\pi(\frac{2}{\sqrt e})^2}{2}\approx 1.338$ (As the radius of inscribed circle $=\frac{2}{\sqrt e}$), no matter what $a$ is :). Any help, such as verification of my discoveries right above, will be appreciate :).
Thank you for your answer(s).