Dog bone-shaped curve: $|x|^x=|y|^y$

Question

EDITED: Some of the questions are ansered, some aren't.

EDITED: In order not to make this post too long, I posted another post which consists of more questions.

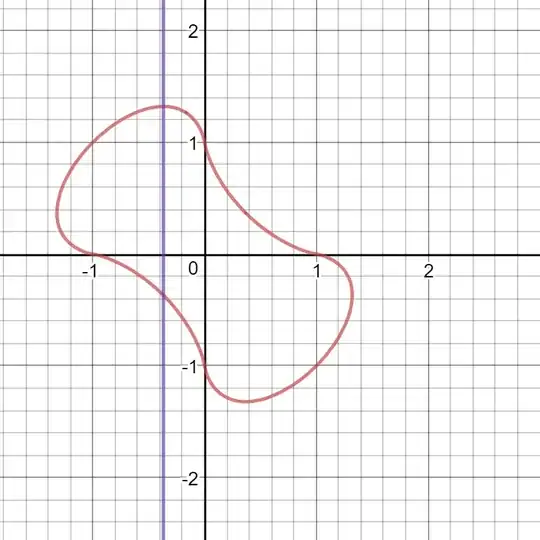
Let $f$ be (almost) the implicit curve$$|x|^x=|y|^y$$ See the graph of the particularly interesting dog bone-shaped curve below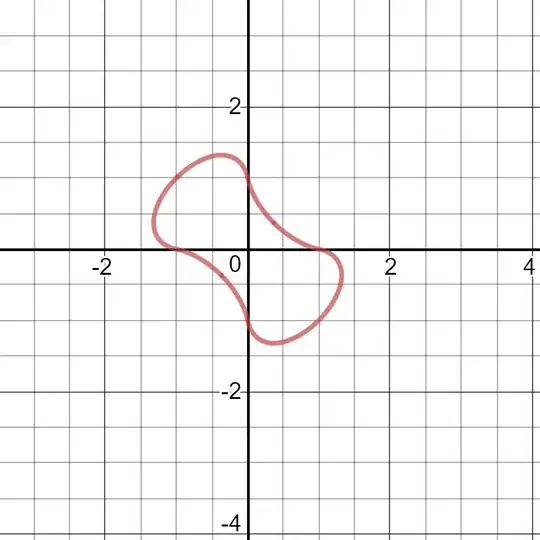Obviously, the graph should contains the line $x=y$.

However, what I want $f$ to be, is, the graph $|x|^x=|y|^y$, without line $x=y$, but nevertheless contains the two points which the curve intersect with $x=y$. Note that the convention $0^0=1$, maybe not as usaul.

Clearly $f$ is not a function.

I doesn't have any idea about continuity, derivative, integral, and many other important technique, apply on an implicit curve.

However, I does want to ask:

$1$) How to write $f$ in an rigorous way? (How to represents 'the intersection of the curve with $x=y$, as the line $x=y$ is originally contains in the curve?)

$2$) Is $f$ continuous?(What does it means to be a continuous implicit curve? Is it smooth?)

$3$) How can we break it down into several functions so that we can use the properties of functions?

$4$)[ANSWERED] Can we find the area (maybe not 'integral', since in definition to Riemann-integral, integral under x-axis is negative, but clearly area can't be negative) surrounding by the curve $f$? Or does it make any sense to say the area of an implicit curve? Is there a strict definition? From wikipedia, maybe we need to show that it is Jordan curve? (Thanks, Peter Heinig, in the comment.
Answer: By Barry Cipra, the integral is $3.527\dots$.

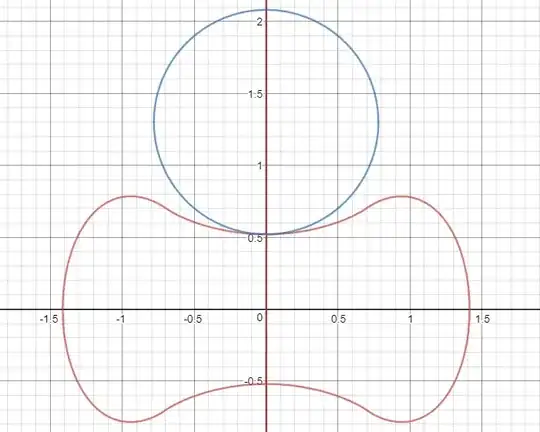
$5$) Given a straight line, at most how many points can the line intersects $f$? I believe the answer is 4, as an example, $y=-x-1$. Moreover, what if the line is in the form $y=a$,while $a\in\mathbb R$? I believe is 2. See the image below, for some example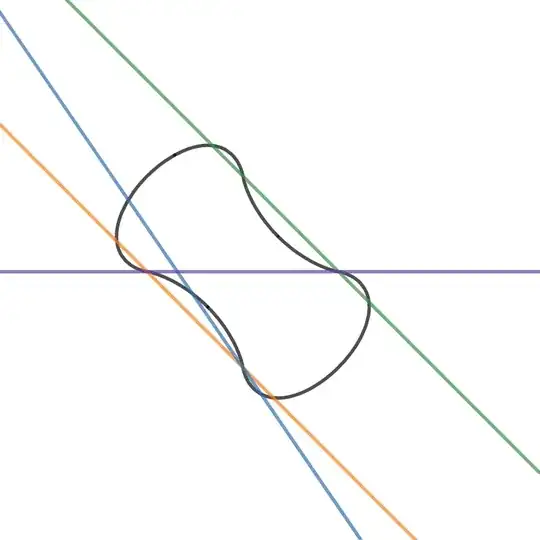

$6$) Where are the extrema of $f$,

• a) in the normal sense,

• b) when we take $x=y$ as the $x$-axis,

• c) when we take $x=-y$ as the $x$-axis?

$7$) What is the intersections of the curve with,

• a) $x=y$, (ANSWERED by Rahul)

• b) $x=-y$, (ANSWERED)

If $x>0$ and $x=−y$, then we get $x^x=x^{−x}$,$x^{2x}=1$,$x=1$,$y=−1$, and similarly for $x<0$ we get $x=−1,y=1$. This answers 7b. – Wojowu

• c) $x$-axis? (ANSWERED)

$8$)

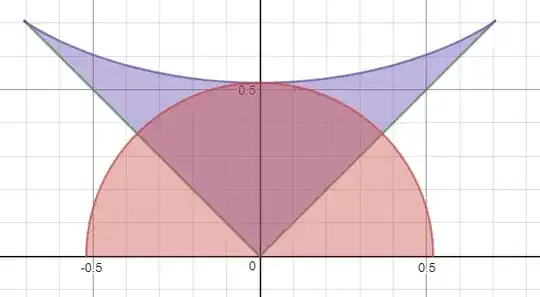
• a) What is the circumscribed circle to the curve $f$? (I think that it may be $x^2+y^2=2$)

• b) What is the inscribed circle to the curve $f$?
  $\space\space\space$(I observed by trial and error that it may be $x^2+y^2=a$
  $\space\space\space$while $a\approx 0.27067056\approx\frac{1352}{4995}$, see the image below)
  

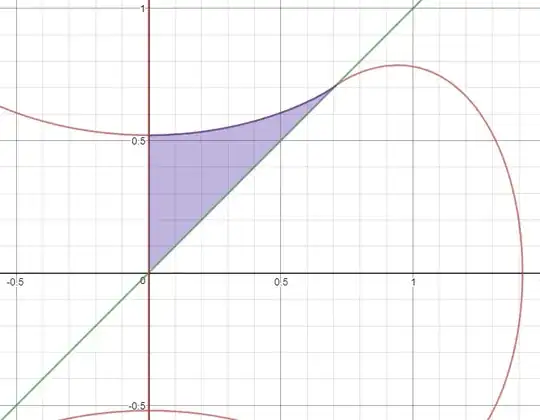
9)[ANSWERED]
Perhaps we should restrict our attention to $x^x=y^y$, consider the part of $f$ which is in the first quadrant (including positive x and y axes),see the image below, the red curve. How can we find the integral of it on [0,1](How can we write it in a more convenient form?) I observed that the integral should be $\gt 1-\frac{\pi}{4}$(See the image below) and $\lt \frac{1}{2}$, perhaps, $\frac{e}{10}$?.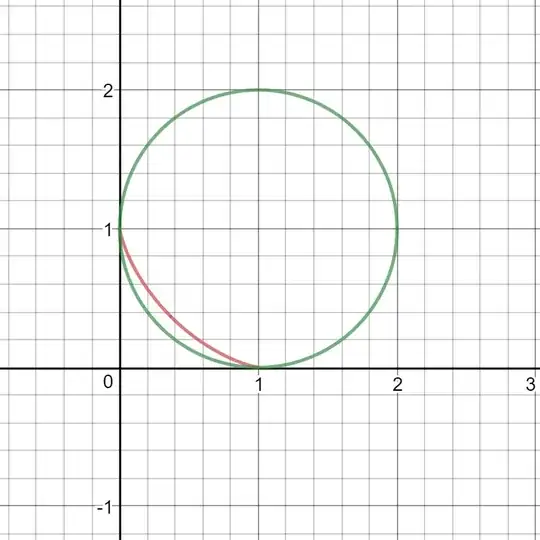
Answer: By Yuriy S, the integral is $0.317\dots$.

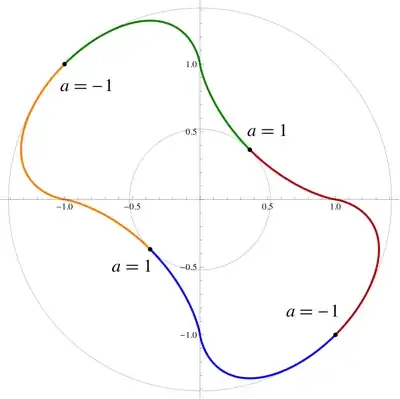
10)Is the locus, when $f$ is rotated around the origin, the area between the two concentric circles $x^2+y^2=2$ and $x^2+y^2=\frac{2}{e^2}$? See the image and here.The equations of the graph:

Using rotation matrix, as mentioned in Yuriy S's answer,
Define a paremeter $a$, as the rotation degree measures in radian (clockwise),
$f$, after rotation, is $$\left|x\cdot\cos a-y\sin a\right|^{x\cdot\cos a-y\sin a}=\left|x\sin a+y\cos a\right|^{x\sin a+y\cos a}$$ For$$\space x\cdot\cos a-y\sin a\neq x\sin a+y\cos a$$Of course, there are two points more.

Does it helps to prove that $f$ is continuous, i.e., question 2 above?

NOTE: To interpret the graph with Desmos, we need to consider two cases, namely, $\space x\cdot\cos a-y\sin a<x\sin a+y\cos a$ and $\space x\cdot\cos a-y\sin a> x\sin a+y\cos a$ respectively, see the link above.

I need really to apologize that I really doesn't have any idea to answer. I am not presently familar with implicit curve, but only a little knowledge about real analysis. However, I ask it because I think it is interesting. Moreover, it is good for an easy answer, but it is not neccesary that the answer should be very elementary, since knowing how the question can be solve by wonderful mathematical techniques is itself interesting. Welcome for any answer, even not as a complete answer to all 10 questions.

Thanks for answering my naive questions!

Sorry for a new question, but I really like to ask :)

Answer 1

There's so many questions... Let me start with a useful hint.

We can rotate the curve $45$ degrees counter clockwise to get something we can better work with.

Rotation can be done with the use of Rotation matrix, which in this case gives us simply:

$$x=\frac{1}{\sqrt{2}} (y_2+x_2) \\ y=\frac{1}{\sqrt{2}} (y_2-x_2)$$

Now we just substitute the above expressions into the equation (and forget about subscripts right after):

$$\left| \frac{1}{\sqrt{2}} (y+x) \right|^{ \frac{1}{\sqrt{2}} (y+x)}=\left| \frac{1}{\sqrt{2}} (y-x) \right|^{ \frac{1}{\sqrt{2}} (y-x)}$$

We get the following plot (with circles added later of course):

The circumscribed circle really has radius $\sqrt{2}$, as the OP guessed. It can be seen by setting $y=0$ in the above equation.

The inscribed circle is more complicated. If we set $x=0$ we get:

$$\left| \frac{y}{\sqrt{2}}\right|^{ \frac{y}{\sqrt{2}}}=\left| \frac{y}{\sqrt{2}}\right|^{ \frac{y}{\sqrt{2}}}$$

But this is true for any $y$. Remember the line $y=x$ which satisfies the original equation? That's why.

By zooming in in Desmos we see that the radius is about $$a \approx 0.52026,$$

see below for the exact value.

---

Now, this kind of equation is very complicated to work with. However, we can use logarithms to make it more manageable:

$$(y+x) \log \left| \frac{1}{\sqrt{2}} (y+x) \right|=(y-x) \log \left| \frac{1}{\sqrt{2}} (y-x) \right|$$

This equation describes the same curve, but now we can work with it using analytical methods (such as Taylor series, in the appropriate ranges of $x$ and $y$).

For example, setting:

$$y>0 \\ y > |x|$$

We can get rid of the absolute values and write:

$$(y+x) \left( \log y+ \log \left(1+\frac{x}{y} \right)-\frac{\log 2}{2} \right)=(y-x) \left( \log y+ \log \left(1-\frac{x}{y} \right)-\frac{\log 2}{2} \right)$$

Simplifying:

$$2x \log y +y \left(1+\frac{x}{y} \right) \log \left(1+\frac{x}{y} \right)- y \left(1-\frac{x}{y} \right) \log \left(1-\frac{x}{y} \right) -x \log 2 =0$$

Now, to find the non-trivial root at $x=0$ (the radius of the inscribed circle) we can add the condition $y \gg |x|$ and expand the logarithmic functions, keeping only the terms up to $x^2$:

$$2x \log y +y \left(1+\frac{x}{y} \right) \left(\frac{x}{y}-\frac{x^2}{2y^2} \right)- y \left(1-\frac{x}{y} \right) \left(-\frac{x}{y}-\frac{x^2}{2y^2} \right) -x \log 2 =0$$

Simplifying (and keeping only the terms up to $x^2$), we get:

$$x \left(2 \log y+2 - \log 2 \right)=0$$

As we've already seen, $x=0$ gives us trivial solution for any $y$. However, if $x \neq 0$, but is very close to it, we have also another solution:

$$2 \log y+2 - \log 2=0$$

$$y=\exp \left( \log \sqrt{2}-1 \right)=\frac{\sqrt{2}}{e}=0.52026009502 \dots$$

This our $a$, radius of the inscribed circle.

---

There's actually another associated circle, which looks like this:

It is completely defined by the curvature of the function around $x=0$.

Its parameters could be deduced exactly (probably) by using the definition of the curvature, but I have used an approximation. Let's keep not only quadratic, but also cubic terms in the logarithm expansion. Then we get:

$$x \left(2 \log y+2 - \log 2-\frac{x^2}{3y^2} \right)=0$$

Rearranging, we can see that (for $x \neq 0$):

$$y=\frac{\sqrt{2}}{e} \exp \left(1+ \frac{x^2}{3y^2}\right) \approx \frac{\sqrt{2}}{e} \left(1+ \frac{x^2}{3y^2}\right)$$

From the general equation of the circle for small $x$ we have:

$$y=y_0-\sqrt{R^2-x^2} \approx y_0-R \left(1- \frac{x^2}{2R^2} \right)=y_0-R+\frac{x^2}{2R}$$

In our case, $R$ is a function of $y$, but let's make another approximation and assume $y= a=\frac{\sqrt{2}}{e}$, then we have:

$$R \approx \frac{3}{e \sqrt{2}} \\ y_0 \approx \frac{5}{e \sqrt{2}}$$

The diagram above uses these values and we can see they fit very well.

---

I'll add more to this once I think of something else.

Answer 2

Parametric Representation

Let $y=ax$, then $$ |x|^x=|ax|^{ax} $$ and therefore, $$ |x|=|a|^{\frac{a}{1-a}} $$ which means that $$ (x,y)=\pm|a|^{\frac{a}{1-a}}(1,a) $$ For $a\not\in[-1,1]$ the transform $a\mapsto\frac1a$, maps $$ \begin{array}{c} a\in(1,\infty)&\pm|a|^{\frac{a}{1-a}}(1,a)&\overset{a\mapsto\frac1a}{\longmapsto}&\pm|a|^{\frac{a}{1-a}}(a,1)&a\in(0,1)\\ a\in(-\infty,-1]&\pm|a|^{\frac{a}{1-a}}(1,a)&\overset{a\mapsto\frac1a}{\longmapsto}&\mp|a|^{\frac{a}{1-a}}(a,1)&a\in[-1,0) \end{array} $$ Thus, we get all of the curve using $a\in[-1,1)$, with the four pieces: $$ \bbox[5px,border:2px solid #C0A000]{ \begin{align} \color{#C00}{+|a|^{\frac{a}{1-a}}(1,a)}\\ \color{#090}{+|a|^{\frac{a}{1-a}}(a,1)}\\ \color{#F90}{-|a|^{\frac{a}{1-a}}(1,a)}\\ \color{#00F}{-|a|^{\frac{a}{1-a}}(a,1)} \end{align} } $$

---

The Circumscribed and Inscribed Circles

The derivative of the log of the distance from the origin is $$ \begin{align} \frac{\mathrm{d}}{\mathrm{d}a}\log\left(|a|^{\frac{a}{1-a}}\sqrt{1+a^2}\right) &=\frac{\frac{1-a^2}{1+a^2}+\log|a|}{(1-a)^2}\\ &\le0 \end{align} $$ since $\frac{1-a^2}{1+a^2}+\log|a|$ is even and increases to $0$ on $(0,1)$; that is, its derivative is $\frac1a\left(\frac{1-a^2}{1+a^2}\right)^2\ge0$. Thus, the distance from the origin decreases monotonically as $a$ goes from $-1$ to $1$. By symmetry, the maximum distance occurs at $a=-1$ and the minimum distance occurs at $a=1$.

The furthest points from the origin, where $a=-1$, are $$ (-1,1)\text{ and }(1,-1) $$ Taking limits, we get the closest points to the origin, where $a\to1^-$, are $$ \left(e^{-1},e^{-1}\right)\text{ and }\left(-e^{-1},-e^{-1}\right) $$ Thus, the radius of the circumscribed circle is $$ \bbox[5px,border:2px solid #C0A000]{\sqrt2} $$ and the radius of the inscribed circle is $$ \bbox[5px,border:2px solid #C0A000]{\frac{\sqrt2}e} $$

---

Area $$ \begin{align} &4\int_{-1}^1\frac12|a|^{\frac{a}{1-a}}(1,a)\times\left[\left(\frac{\mathrm{d}}{\mathrm{d}a}|a|^{\frac{a}{1-a}}\right)(1,a)+|a|^{\frac{a}{1-a}}(0,1)\right]\mathrm{d}a\\ &=2\int_{-1}^1|a|^{\frac{2a}{1-a}}\,\mathrm{d}a\\[6pt] &\doteq\bbox[5px,border:2px solid #C0A000]{3.5272349603958296088} \end{align} $$

---

Length

We could avoid computing the following derivative for the area because $(1,a)\times(1,a)=0$, but we need it for the length: $$ \frac{\mathrm{d}}{\mathrm{d}a}|a|^{\frac{a}{1-a}} =\frac{1-a+\log|a|}{(1-a)^2}|a|^{\frac{a}{1-a}} $$ Thus $$ \begin{align} \left|\,\frac{\mathrm{d}}{\mathrm{d}a}\left(|a|^{\frac{a}{1-a}}(1,a)\right)\,\right| &=|a|^{\frac{a}{1-a}}\left|\frac{1-a+\log|a|}{(1-a)^2}(1,a)+(0,1)\right|\\ &=|a|^{\frac{a}{1-a}}\left[\left(\frac{1-a+\log|a|}{(1-a)^2}\right)^2+\left(a\frac{1-a+\log|a|}{(1-a)^2}+1\right)^2\right]^{1/2}\\ &=\frac{|a|^{\frac{a}{1-a}}}{(1-a)^2}\sqrt{(1-a+\log|a|)^2+(1-a+a\log|a|)^2} \end{align} $$ Therefore, $$ 4\int_{-1}^1\left|\,\frac{\mathrm{d}}{\mathrm{d}a}\left(|a|^{\frac{a}{1-a}}(1,a)\right)\,\right|\mathrm{d}a \doteq\bbox[5px,border:2px solid #C0A000]{8.0060888731054946925} $$

---

Maximum $\boldsymbol{y}$

Letting $t=-a$ where $a\lt0$, on the green curve, we wish to find the maximum, for $t\gt0$, of $$ \log\left(t^{-\frac{t}{1+t}}\right)=-\frac{t}{1+t}\log(t) $$ Taking the derivative, gives $$\newcommand{\W}{\operatorname{W}} -\frac1{(1+t)^2}\log(t)-\frac1{1+t}=0\implies t=\W\left(\frac1e\right) $$ Thus, the maximum $y$ is $$ \bbox[5px,border:2px solid #C0A000]{t^{-\frac{t}{1+t}}\doteq1.321099762015617457} $$ which happens when $x=-ty$; that is, when $x$ is $$ -t^{\frac1{1+t}}\doteq-0.36787944117144232160 $$ The other non-rotated extremal points can be found by symmetry.

---

Answer 3

Let's use polar coordinates to examine some of the aspects of the dogbone. Writing $x=r\cos\theta$ and $y=r\sin\theta$, with $r\gt0$ and $0\le\theta\lt2\pi$ for $(x,y)\not=(0,0)$, we find

$$|x|^x=|y|^y\iff x\ln|x|=y\ln|y|\iff \cos\theta(\ln r+\ln|\cos\theta|)=\sin\theta(\ln r+\ln|\sin\theta|)\\ \iff(\cos\theta-\sin\theta)\ln r=\sin\ln|\sin\theta|-\cos\theta\ln|\cos\theta|$$

so generically we have

$$\ln r={\sin\theta\ln|\sin\theta|-\cos\theta\ln|\cos\theta|\over \cos\theta-\sin\theta}$$

or

$$r(\theta)=\left(|\sin\theta|^{\sin\theta}\over|\cos\theta|^{\cos\theta} \right)^{1/(\cos\theta-\sin\theta)}$$

This is well defined and continuous for all values of $\theta$ except when $\cos\theta=\sin\theta$, i.e., at $\theta={\pi\over4}$ and ${5\pi\over4}$. (Note, the equation $(\cos\theta-\sin\theta)\ln r=\sin\ln|\sin\theta|-\cos\theta\ln|\cos\theta|$ allows $r$ to take on any positive value when $\cos\theta=\sin\theta$, giving us all points on the line $y=x$, but we are ignoring those points, except for the ones that are on the curve.) L'Hopital allows us to fill in a value for $\ln r$ at those points. By symmetry, it suffices to look at $\theta\to\pi/4$. We get

$$\begin{align} \lim_{\theta\to\pi/4}{\sin\theta\ln|\sin\theta|-\cos\theta\ln|\cos\theta|\over \cos\theta-\sin\theta} &=\lim_{\theta\to\pi/4}{(\cos\theta\ln|\sin\theta|+\cos\theta)+(\sin\theta\ln|\cos\theta|+\sin\theta)\over-\sin\theta-\cos\theta}\\ &=\ln\sqrt2-1 \end{align}$$

which tells us

$$r\left(\pi\over4\right)={\sqrt2\over e}\approx0.52026$$

as Yuriy S found.

We can also ask Wolfram Alpha to evaluate the integral for the area:

$$A=\int_0^{2\pi}{1\over2}r(\theta)^2\,d\theta=\int_0^\pi\left(|\sin\theta|^{\sin\theta}\over|\cos\theta|^{\cos\theta} \right)^{2/(\cos\theta-\sin\theta)}d\theta\approx3.52723$$

Answer 4

This is for question 9). I'm posting another answer, because my first one has become bloated enough.

To find the integral, I will use my rotated function again. It's not hard to see that the area the OP wants to find is twice the shaded area:

To write the integral explicitly, I will use the equation I obtained for $y>x$ and $y>0$:

$$2x \log y +y \left(1+\frac{x}{y} \right) \log \left(1+\frac{x}{y} \right)- y \left(1-\frac{x}{y} \right) \log \left(1-\frac{x}{y} \right) -x \log 2 =0$$

Let's introduce a new parameter:

$$t=\frac{x}{y}, \qquad t \in (0,1)$$

Then, we have an explicit function:

$$\log y(t)= \frac{\log 2}{2}-\frac{1}{2}\left(\frac{1}{t} +1\right) \log (1+t)+\frac{1}{2} \left( \frac{1}{t}-1 \right) \log (1-t)$$

Note that:

$$y(1)=\frac{1}{ \sqrt{2} }$$

The shaded area is given by:

$$I= \int_0^{1/ \sqrt{2}} y(x) dx - \int_0^{1/ \sqrt{2}} x dx=\int_0^{1/ \sqrt{2}} y(x) dx- \frac{1}{4}$$

It's important to note:

$$dx=d(t y)=t \frac{dy}{dt} dt+y dt= \left(t \frac{dy}{dt}+y \right) dt$$

So we have:

$$\int_0^{1/ \sqrt{2}} y(x) dx=\int_0^1 y(t) \left(t \frac{dy}{dt}+y \right) dt=\int_0^1 t y \frac{dy}{dt} dt+\int_0^1 y^2 dt$$

The first integral can be computed integrating by parts:

$$J=\int_0^1 t y \frac{dy}{dt} dt=t y^2 \big|_0^1 - \int_0^1 y(t) \left(t \frac{dy}{dt}+y \right) dt= \frac{1}{2}-J - \int_0^1 y^2 dt$$

Which means:

$$J=\frac{1}{4}-\frac{1}{2} \int_0^1 y^2 dt$$

And finally:

$$I=\frac{1}{2} \int_0^1 y^2 dt$$

$$I=\int_0^1 \exp \left(- \left(\frac{1}{t} +1\right) \log (1+t)+ \left( \frac{1}{t}-1 \right) \log (1-t) \right) dt \tag{1}$$

Wolfram Alpha computes:

$$I=0.15858185771988216006213921681874564 \dots$$

So finally the area the OP was interested in:

$$2I=0.31716371543976432\dots$$

---

I hope I haven't made any mistakes, but at least the OP's estimates check out as:

$$1-\frac{\pi}{4} < 2I < \frac{1}{2}$$

Update:

The value is correct, as confirmed by using Barry Cipra's polar form:

$$2I=\int_0^{\pi/4}\left(|\sin\theta|^{\sin\theta}\over|\cos\theta|^{\cos\theta} \right)^{2/(\cos\theta-\sin\theta)}d\theta$$

Update 2

A little workings with the integral (1). Using the Taylor series for the logarithm and simplifying, we get a very compact formula with the series:

$$I=\frac{1}{e^2} \int_0^1 \exp \left( \sum_{k=1}^\infty \frac{t^{2k}}{k(2k+1)} \right) dt= \\ =\frac{1}{e^2} \int_0^1 \exp \left( \frac{t^2}{3}+\frac{t^4}{10}+\frac{t^6}{21}+\frac{t^8}{36}+\frac{t^{10}}{55}+\cdots \right) dt \tag{2}$$

This gives $\frac{2}{e^2}$ (which is precisely $a^2$, i.e. the radius of the inscribed circle) as a good approximation (from below) to the area in question. The integral in (2) has a value of about $1.17$.

Here's for comparison, the area of half the inscribed circle $A_1= a^2 \frac{\pi}{2}$ and the area found here $A_2 = a^2 \int_0^1 \exp \left( \sum_{k=1}^\infty \frac{t^{2k}}{k(2k+1)} \right) dt$:

---

For a more complete description, alternative to the polar one, I will also add parametric form for $x>y$, which is derived in the same way from the logarithmic equation.

Now the complete parametric representation of the curve is:

$$\begin{cases} \displaystyle x(t)= \pm \frac{\sqrt{2}}{e}~t ~ \exp \left( \sum_{k=1}^\infty \frac{t^{2k}}{2k(2k+1)} \right) \\ \displaystyle y(t)= \pm \frac{\sqrt{2}}{e} \exp \left( \sum_{k=1}^\infty \frac{t^{2k}}{2k(2k+1)} \right) \\ t \in (0,1) \end{cases} \tag{a}$$

$$\begin{cases} \displaystyle x(t)= \pm \sqrt{2} \exp \left( -\sum_{k=1}^\infty \frac{t^{2k}}{2k(2k-1)} \right) \\ \displaystyle y(t)= \pm \sqrt{2}~ t ~ \exp \left(- \sum_{k=1}^\infty \frac{t^{2k}}{2k(2k-1)} \right) \\ t \in (0,1) \end{cases} \tag{b}$$

As you can see, it consists of $8$ pieces, for each sign in (a) and (b).

Using this representation, one can explicitly compute arclength of the curve.

Here's the Desmos link with the demonstration.

From the symmetry properties we have for the whole area (in agreement with the results of Barry Cipra and robjohn):

$$A=4 \int_0^1 \left( \frac{1}{e^2} \exp \left(\sum_{k=1}^\infty \frac{t^{2k}}{k(2k+1)} \right) + \exp \left(- \sum_{k=1}^\infty \frac{t^{2k}}{k(2k-1)} \right)\right) dt =3.52723\dots $$

Answer 5

And by using the Rotation matrix which Yuriy S did, the rotated curve which as y=-x as the x axis,it can be descibed as $$|\frac{1}{\sqrt2}(y+x)|^{\frac{1}{\sqrt2}(y+x)}=|\frac{1}{\sqrt2}(y-x)|^{\frac{1}{\sqrt2}(y-x)}$$ This newly rotated curve is symmetric about the x axis and the y axis, so it's extrema on the first quadrant is can be quadruplicated by symmetrically moving them. Therefore, i will only consider when $y>0, x>0, |y|<|x|$(by the graph)

By applying logarithm, it turns to $$(y+x)\ln(\frac{1}{\sqrt2}(y+x))=(y-x)\ln(\frac{1}{\sqrt2}(x-y))$$

$$(y+x)\ln(y+x)-\frac{1}{2}(y+x)\ln2=(y-x)\ln(x-y)-\frac{1}{2}(y-x)\ln2$$

In order to differentiate the with x, making the expression simpler, $$y(\ln(y+x)-\ln(x-y))+x(\ln(y+x)+\ln(x-y)-\ln2)=0$$ $$\frac{dy}{dx}(\ln(y+x)-\ln(x-y))+y(\frac{1+\frac{dy}{dx}}{y+x}-\frac{-1+\frac{dy}{dx}}{y-x})+\ln(y+x)+\ln(x-y)-\ln2+x(\frac{1+\frac{dy}{dx}}{y+x}+\frac{-1+\frac{dy}{dx}}{y-x})=0$$

We are interested when $\frac{dy}{dx}=0$, so

$$\frac{y}{y+x}+\frac{y}{y-x}+\ln(y+x)+\ln(y-x)-\ln2+\frac{x}{y+x}-\frac{x}{y-x}=0$$ Therefore, $2-\ln2+\ln(x^2-y^2)=0, \ x^2-y^2=\frac{2}{e^2}$

I'm thinking about how to find the root of this...

I first thought about rotating $x^2-y^2=\frac{2}{e^2}$ and find the intersecting point with $|x|^x=|y|^y$, but this is the same thing with finding the points where $\frac{dy}{dx}=-1$ on the original curve. If i rotate $x^2-y^2=\frac{2}{e^2}$ $\frac{\pi}{4}$ clockwise, the hyperbola changes into $$xy=-\frac{1}{e^2}$$

Therefore, we can let $$y=-\frac{1}{xe^2}$$

Since $x<0 \ and y>0$due to the graph, $$x\ln(-x)=y\ln y$$ $x\ln(-x)=\frac{1}{xe^2}(\ln(-x)+2)$

WolframAlpha computes $x\approx-0.110838771758797...$ or $-1.22101031154625...$ This value is right because the two points should be symmetric about $y=x$, and they are(using $xy=-\frac{1}{e^2}$)

Lastly, if we rotate $(-0.110838771758797, 1.22101031154625)$ again, the point is $$(-0.941759518322086, 0.785009824064019)$$

The second way was to find where $\frac{dy}{dx}=-1$, which can be calculated by:

$$(-x)^x=y^y,\ x\ln(-x)=y \ln y,\ \ln(-x)+1=\frac{dy}{dx}(\ln y+1)$$ $$\ln(-xy)=-2,\ xy=\frac{-1}{e^2}$$

This way was much easier, without needing to use the rotation matrix(although you need to find rotate the point at the end).

Answer 6

There is a point that has not been mentioned so far: The dogbone curve is only $C^1$ at its inflection points. In fact the curvature does not assume the value $0$ at these points, but tends to $\pm\infty$ when approaching such a point from either side.

Consider the inflection point ${\bf p}=(0,1)$, and put $$x\log|x|=y\log y=: t\ .$$ Writing $y=1+u$ with $|u|\ll1$ near ${\bf p}$ we have $$t=(1+u)\log(1+u)=u+{u^2\over2}-{u^3\over6}+\ldots=:f(u)\ ,$$ whereby $f$ is analytic in a neighborhood of $u=0$, with $f(0)=0$ and $f'(0)=1$. It follows that $f$ has an inverse function $g$, defined in a neighborhood of $t=0$, and we have $$u=g(t)=t-{t^2\over2}+{2t^3\over3}-\ldots\quad.$$ We then can write our dogbone curve in the neighborhood of ${\bf p}$ in the form $$y=1+g\bigl(x\log|x|\bigr)=:h(x)\ .$$ Using the formula $$\kappa(x)={h''(x)\over\bigl(1+h'^2(x)\bigr)^{3/2}}$$ it is then easy to verify that $\lim_{x\to\pm0}\kappa(x)=\pm\infty$.

Answer 7

For 6a), we know that that dog-bone shaped curve has some extrema on the second and fourth quadrant, so let's differentiate that.

Clearly, this curve is symmetric about $y=x$, so I will consider only on the second quadrant, where $x<0$ and $y>0$.

$$(-x)^{x}=y^y$$ $$x\ln(-x)=y\ln y$$ $$\ln(-x)+1=\{\ln y+1\}\frac{dy}{dx}$$

we need to find where $\frac{dy}{dx}=0$, so $$\ln(-x)+1=0$$ $$x=-e^{-1}$$

I don't know how to post images, but by usng desmos, it's clear that $|x|^x=|y|^y$has its extrema on $x=-1/e, 1/e$ $\ \ $ $y^y=e^{1/e}, y\approx1.3211$(I found that with trial and error on the xy plane.)

In same way, we can know that the domain and the range of the curve(excluding y=x) is $\{-1.3211\le x \le 1.3211\},\ \{-1.3211\le y \le 1.3211\}$

Answer 8

I'm quite confused why many people just "take it for granted" that the circumscribed circle will pass $(-1, 1)$. If the slope of the tangent is close to -1(that is to say, $\frac{dy}{dx}|_{x=-1} \approx-1$),the circle might not pass $(-1,1)$, just like a chord.

I'll admit, I maybe quite preoccupied and this doesn't need to be 'proved'(or it has ben, but I couldn't notice), but I wanted to "prove" that the radius of the inscribed and circumscribed circle is what people above calculated.

So, thanks to Barry Cipra, we all know that the dog-boned curve can be presented as a following polar coordinates:$$r(\theta)=(\frac{|\sin(\theta)|^{\sin(\theta)}}{|\cos(\theta)|^{\cos(\theta)}})^{\frac{1}{\cos\theta-\sin\theta}}$$ $$\ln r(\theta)=\frac{\sin\theta \ln|\sin\theta|-\cos\theta \ln|\cos\theta|}{\cos\theta-\sin\theta}$$

For the circumscribed circle, the $\frac{\pi}{2}<\theta<\pi$ $$\frac{1}{r(\theta)}\frac{d}{d\theta}r(\theta)=\frac{\ln(\sin\theta)-\ln(-\cos\theta)}{(\cos\theta-\sin\theta)^{2}}$$ When $\theta=\frac{3}{4}\pi$, $r(\theta)$has it's maximum value because $\frac{dr(\theta)}{d\theta}=0$, and $$r(\frac{3}{4}\pi)=\sqrt2$$

In same way, for the inscribed circle, $\frac{dr(\theta)}{d\theta}=\pm\infty$ when $\theta=\frac{\pi}{4}$, so there's the local minimum point of $r(\theta)$, so the radius of the inscribed circle is $\frac{\sqrt2}{e}$

Answer 9

For 7c), it is easy, let me do it by myself.

The question can be reduced to the solution of equation $0^0=1=\vert x\vert ^x$. Consider $g(x)=x^x$, defined on $\mathbb R^+$. $$0<x<1\implies g(x)<1$$and $$x>1\implies g(x)>1$$therefore$$g(x)=1\implies x=1$$, also, $$x^{-x}=1 \land x\in\mathbb R^+\implies x=1$$See the image below
Therefore, $$0^0=\vert x\vert ^x\implies x=\pm 1 \lor x=0\space (rejected)$$To conclude, the intersections of $f$ and $y=0$ are (-1,0) and (1,0).

Answer 10

Question 1

One way to answer your first question is to formulate it as an Analytic Variety. An analytic variety of a single function on the field $\mathbb{R}^2$ is defined as the set, $$ A(f) = \{ (x,y) \in \mathbb{R}^2 | f(x,y) = 0 \} $$

In the case of the proposed equation, $$ |x|^x = |y|^y $$

One can define a function, $$ \begin{align} f : \mathbb{R}^2 \rightarrow& \mathbb{R} \\ (x,y) \mapsto& |x|^x - |y|^y \end{align} $$

the line ($y=x$) would be, $$ \begin{align} g : \mathbb{R}^2 \rightarrow& \mathbb{R} \\ (x,y) \mapsto& x - y \end{align} $$

Since the zeros of the equation $|x|^x = |y|^y$ include the solutions of $y=x$. The intersection is written as $A(f)\cap A(g) = A(g)$. The dog bone shape alone is $(A(f) \setminus A(g)) \cup \{(1,1), (-1,-1) \}$.

Question 2

Continuity does not have the same meaning in a set, even though the resulting curves look like functions. For example, a variety could be the intersection of a plane passing through the origin and a torus. Although it is locally path-connected there would be two disjoint circles, making it, in some sense, discontinuous.

To analyse the curve differentially one needs to use Reimannian Geometry. If it is a curve in the traditional sense, then it will conform to the definition of a manifold. Your example is a Reimannian manifold of dimension $1$ because it is locally homeomorphic to $[0,1]$. The local homeomorphisms are known as charts. Barry Cipra gave,

$$ \begin{align} h : [0, 2\pi) \rightarrow& A(f) \\ \theta \mapsto& r(\theta)\left( \begin{array}{c} \cos{\theta} \\ \sin{\theta} \end{array} \right) \end{align} $$ where, $$ \begin{align} r : [0, 2\pi) \rightarrow& \mathbb{R} \\ \theta \mapsto& \left( \frac{|\sin{\theta}|^{\sin{\theta}}}{|\cos{\theta}|^{\cos{\theta}}} \right)^{\frac{1}{\cos{\theta} - \sin{\theta}}} \end{align} $$

as a homeomorphism between $[0, 2\pi)$ and $A(f)$, and so $A(f)$ is locally homeomorphic to $[0,1]$.

The manifold is called smooth if every local homeomorphism is smooth, which is also provable using the same parametrisation.