Reflect a ray off a circle so it hits another point

Question

my problem is the following:

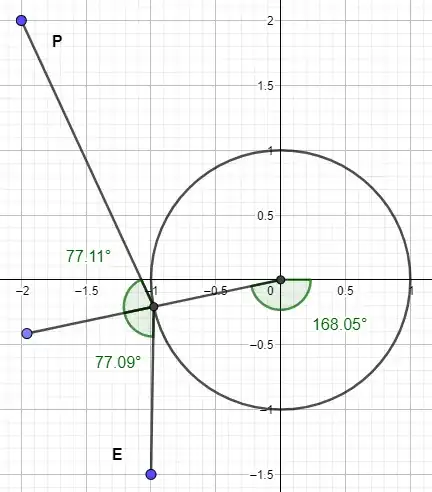
I have two points ($e$ and $p$) in a 2D space and I am trying to figure out where on the circle is the reflection of $p$ as seen from $e$. $$$$ $$$$ So the way I approached this is by looking for the vector from the center of the circle to the point, where the ray is reflected.

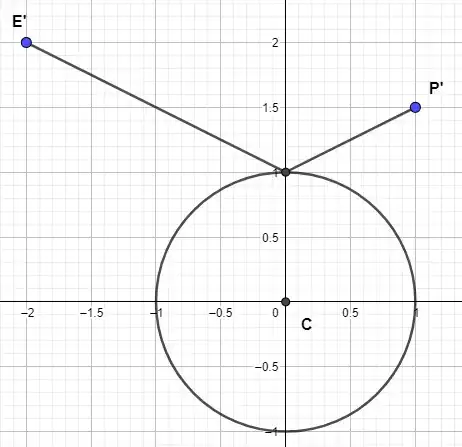
[For simplicity the circle's center is located at $\color{darkturquoise}{(0,0)}$ and it has a radius with unit length. The two points are represented by the vectors $\color{deeppink}{e}$ and $\color{gold}{p}$]

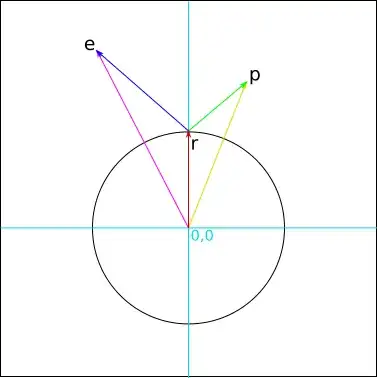
In the picture were looking for the vector $\color{red}{r}$, which coincides with the normal vector of the surface of the circle. So this vector has to fulfill 2 properties:

1. $||\color{red}{r}|| = 1$
2. The angle between $\color{red}{r}$ and $\color{green}{p-r}$ should be equal to the angle between $\color{blue}{e-r}$ and $\color{red}{r}$.

The equation for the fist property is pretty straight forward. For the second property I came up with the following equation: $$\Bigg|\Bigg|\frac{\color{blue}{e-r}}{||\color{blue}{e-r}||}\times\color{red}{r}\Bigg|\Bigg| = \Bigg|\Bigg|\color{red}{r}\times\frac{\color{green}{p-r}}{||\color{green}{p-r}||}\Bigg|\Bigg|\\ \frac{||(\color{blue}{e-r})\times\color{red}{r}||}{||\color{blue}{e-r}||} =\frac{||\color{red}{r}\times(\color{green}{p-r})||}{||\color{green}{p-r}||}\\ \frac{1}{||\color{blue}{e-r}||}\Big|\Big|(\color{deeppink}{e}\times\color{red}{r})-\big((-\color{red}{r})\times\color{red}{r}\big)\Big|\Big|= \frac{1}{||\color{green}{p-r}||}\Big|\Big|(\color{red}{r}\times\color{gold}{p})-\big(\color{red}{r}\times(-\color{red}{r})\big)\Big|\Big|\\ \frac{||\color{deeppink}{e}\times\color{red}{r}||}{||\color{blue}{e-r}||}= \frac{||\color{red}{r}\times\color{gold}{p}||}{||\color{green}{p-r}||}\\ \frac{||\color{green}{p-r}||}{||\color{blue}{e-r}||}= \frac{||\color{red}{r}\times\color{gold}{p}||}{||\color{deeppink}{e}\times\color{red}{r}||}\\ \frac{\sqrt{1 + ||\color{deeppink}{e}||^{2} - 2(\color{red}{r}\cdot\color{pink}{e})}}{\sqrt{1 + ||\color{gold}{p}||^{2} - 2(\color{red}{r}\cdot\color{gold}{p})}}= \frac{||\color{red}{r}\times\color{gold}{p}||}{||\color{deeppink}{e}\times\color{red}{r}||} $$ After that I use the fact that the cross product of 2 2D-Vectors has a single non-zero value and it determines the length of that cross product. $$ \frac{\sqrt{1 + ||\color{deeppink}{e}||^{2} - 2(\color{red}{r}_{1}\color{pink}{e}_{1} + \color{red}{r}_{2}\color{pink}{e}_{2})}}{\sqrt{1 + ||\color{gold}{p}||^{2} - 2(\color{red}{r}_{1}\color{gold}{p}_{1} + \color{red}{r}_{2}\color{gold}{p}_{2})}}= \frac{\color{red}{r}_{1}\color{gold}{p}_{2}-\color{red}{r}_{2}\color{gold}{p}_{1}}{\color{deeppink}{e}_{1}\color{red}{r}_{2}-\color{deeppink}{e}_{2}\color{red}{r}_{1}} $$ The left hand side is positive. I want both angles to have equal signs, because they are both in the same general direction as $\color{red}{r}$. This means that the right hand side is also positive. I square both sides to get rid of the roots on the left. $$ \frac{1 + ||\color{deeppink}{e}||^{2} - 2(\color{red}{r}_{1}\color{deeppink}{e}_{1} + \color{red}{r}_{2}\color{pink}{e}_{2})}{1 + ||\color{gold}{p}||^{2} - 2(\color{red}{r}_{1}\color{gold}{p}_{1} + \color{red}{r}_{2}\color{gold}{p}_{2})}= \frac{(\color{red}{r}_{1}\color{gold}{p}_{2}-\color{red}{r}_{2}\color{gold}{p}_{1})^{2}}{(\color{deeppink}{e}_{1}\color{red}{r}_{2}-\color{deeppink}{e}_{2}\color{red}{r}_{1})^{2}} $$ And this is as far as I can get. I don't think substituting $p_{2}$ with $\sqrt{1-p_{1}^2}$ will get me anywhere and also avoid it, since I am going to use that in a graphic application and I am trying to make as few calculations as possible.$$$$ Hope I explained the problem well enough and followed all conventions on this forum :) This is my first post here, so I accept any critique on it.

Answer 1

I have made a Geogebra model (https://www.geogebra.org/m/r75cgAfw ) that works according to your original equations and seems to give the right answers as far as tested. Starting with your originals: The angle between $r$ and $p-r$ should be equal to the angle between $r$ and $e-r$ $$acos\left(\frac{\mathbf{r-(p-r)}}{\mathbf{|r|\cdot|p-r|}}\right)=acos\left(\frac{\mathbf{r-(e-r)}}{\mathbf{|r|\cdot|e-r|}}\right)$$ $$|r|=1$$

Next I need to simplify some, so 1) expand the numerator and 2)replace both |r| and r\cdot r with 1, and 3)drop the acos from both sides. to get: $$\mathbf{\frac{r\cdot p-1}{|p-r|}}=\mathbf{\frac{r\cdot e-1}{|e-r|}}$$

Next, I substitute the vector (x,y) for $\mathbf r$ remembering that both $\mathbf e$ and $\mathbf p$ are known vectors. $$\frac{p_{x}x+p_{y}y-1}{\sqrt{(p_{x}-x)^{2}+(p_{y}-y)^{2}}}=\frac{e_{x}x+e_{y}y-1}{\sqrt{(e_{x}-x)+(e_{y}-y)^{2}}}$$ Finally, substitue in $x=\sqrt{-y^2+1}$ for x. That creates a minor issue with where on the circle the reflection is, since it causes 2 answers, one on each side of the circle. Still, the CAS equation to Geogebra is $$\frac{p_{y} y + \sqrt{-y^{2} + 1} p_{x} - 1}{\sqrt{{\left(p_{x} -\sqrt{-y^{2} + 1}\right)}^{2} + {\left(p_{y} - y\right)}^{2}}} =\frac{e_{y} y + \sqrt{-y^{2} + 1} e_{x} - 1}{\sqrt{{\left(e_{x} -\sqrt{-y^{2} + 1}\right)}^{2} + {\left(e_{y} - y\right)}^{2}}}$$ which is 1 equation in 1 unknown, thus allowing a relatively fast numeric solution. Fast enough that one can move around points E and P and get various solutions.

Answer 2

Made a program which seems to work very well, i.e. it has passed all the examples I have tried. It uses no iteration but does require solving a cubic polynomial. I'll provide the code if you are interested.

My idea is the following: If I rotate the points E and P around the circle center, then at some rotation angle $\alpha$ the point of reflection must be at the top of the circle, i.e. at the point $(0,1)$. And a way to know I have found the right rotation angle is if the slope of a line from E' to $(0,1)$ is the negative equal of the slope from P' to $(0,1)$. If I could find the angle in this way, then the point of reflection, in the original setup, would just be located at an angle of $\frac{\pi}{2} - \alpha$.

So, if we let $E=(a,b)$ and $P=(c,d)$, then the rotated position of $E$, call it $E'=(a_1, b_1)$, would be:$$a_1 = a \cos(\alpha)-b \sin(\alpha)$$ $$b_1 = a \sin(\alpha)+b \cos(\alpha)$$ Same goes for $P'=(c_1,d_1)$.

If the slopes from $E'$ and $P'$ to (0,1) are negative equals, then $$\frac{b_1-1}{a_1} = -\frac{d_1-1}{c_1}$$

Inserting the equations for $a_1, b_1,$ etc into the equation above and simplifying, we get $$(ac-bd)\sin(2\alpha) + (bc+ad) \cos(2\alpha)+(b+d) \sin(\alpha) -(a+c)\cos(\alpha) = 0$$ Not so easy to solve. But, I decided to try an approximation, simply substituting the trig functions with the first two terms of their Taylor series. These are quite accurate up to about $40^\circ$, which is enough as I'll later talk about.

Inserting the substitutions and simplifying we get $$-\frac{8e+g}{6}\alpha^3 + (\frac{h}{2}-2f)\alpha^2+(2e+g)\alpha+(f-h) = 0$$ where $e=(ac-bd), f=(bc+ad), g=(b+d)$ and $h=(a+c)$.

The roots of this cubic equation can now be found in the usual manner.

This was my first version of the program and it worked somewhat, but could be off by $5-6 ^\circ$ which is too much. The problem is that the approximations get inaccurate for large angles. The solution I found was to do an initial rotation of E and P such that the angle bisector of $\angle E'CP'$ is at $90^\circ$. This puts E and P close to where they should be and means the final adjustment angle to be found via the cubic equation, is small.

Based on the examples I've tried (and checked via GeoGebra drawings), the accuracy of the found angle is now close to 2 decimal places. An example below:

The input was $E=(-1,-1.5), P=(-2,2)$ and the ouput was the angle $-168.05^\circ$.

Answer 3

I'm going to report the result I got from some quick calculations, in case someone can take them further. The result is kind of neat, but it doesn't seem to lead to any nice closed answer so the OP, who probably values speed of calculation over absolute accuracy, should probably go with other methods.

Call the points $p$ and $e$ as $\vec a$ and $\vec b$. (It doesn't matter which is which, as the configuration is symmetric in $\vec a$ and $\vec b$.) Let $\vec u$ be the unit vector to the point on the circle and $r$ be the radius of the circle. I calculated the direction of the line you get by bouncing $\vec a - r\vec u$ off the point $r\vec u$, and then wrote the equation requiring $\vec b$ to lie on the line in that direction passing through $r \vec u$. If we write $\vec v ^\perp$ for the vector $\vec v $ rotated 90 degrees (counter-clockwise, to pick a definite direction) the equation simplifies to $$2(\vec a\cdot \vec u)(\vec b \cdot \vec u ^\perp) - r(\vec b \cdot \vec u ^\perp) + r(\vec a ^ \perp \cdot \vec u) = \vec b \cdot \vec a ^ \perp.$$

If you were to write $\vec u$ as $(\cos\theta, \sin \theta)$ and plug it in to the equation you'd get a "trigonometric quadratic", i.e. it would have $\cos$, $\sin$, $\cos^2$, $\cos\cdot\sin$, and $\sin^2$ terms. I'm sure you could find an algorithm for solving these types of equations, but I'm also guessing it'd be to messy to be useful in your situation.

Answer 4

Fermat’s principle suggests an approach to this problem. The idea is to find the point $\mathbf r$ on the circle that minimizes the distance $\|\mathbf r-\mathbf p\|+\|\mathbf r-\mathbf e\|.$ Using the parameterization $\mathbf r=(r\cos t,r\sin t)$, this distance is $$\sqrt{(\cos t-p_x)^2+(\sin t-p_y)^2}+\sqrt{(\cos t-e_x)^2+(\sin t-e_y)^2}$$ and the problem becomes that of solving $${p_x\sin t-p_y\cos t \over \sqrt{(\cos t-p_x)^2+(\sin t-p_y)^2}}+{e_x\sin t-e_y\cos t \over \sqrt{(\cos t-e_x)^2+(\sin t-e_y)^2}} = 0.$$ Unfortunately, this doesn’t appear to lend itself to a nice (or even not so nice) closed-form solution. Rahul’s suggestion of binary search or perhaps a Newton’s method approximation to the root of the equation seems best for a practical solution that is to be coded. The angle bisector of $\mathbf p$ and $\mathbf e$ is a reasonable first guess for $t$ (equiv. $\mathbf r$) for any such iterative approximation.

A perhaps more promising approach that comes to mind is that the point $\mathbf r$ is such that $\mathbf p$, $\mathbf r$ and the reflection of $\mathbf e$ in the tangent at $\mathbf r$ are colinear. (By symmetry, you could reflect $\mathbf p$ instead, of course.) A normal vector to the tangent at $\mathbf r$ is $\mathbf r$ itself, so the reflection of $\mathbf e$ is $$\mathbf e' = \mathbf e + 2(1-\mathbf e\cdot\mathbf r)\,\mathbf r.$$ The colinearity condition can be expressed via the vanishing of the scalar triple product (in homogeneous coordinates) $[\mathbf r,\mathbf p,\mathbf e']=0$. Expanding by coordinates, this translates into the equation $$(p_x e_y+p_y e_x)(x^2-y^2) - 2(p_x e_x-p_y e_y)xy - (p_y+e_y)x + (p_x+e_x)y = 0. \tag{*}$$ Together with the constraint $x^2+y^2=1$, this makes the problem that of computing the intersection(s) of this hyperbola with the unit circle. There’s an unavoidable cubic equation that needs to be solved, but the entire computation can be mechanized via an algorithm described in Richter-Gebert’s Perspectives on Projective Geometry and sketched out in this answer. Since one of the conics is a unit circle, there are likely some simplifications that can be made to the general computation. There can be up to four intersections, so you’ll still need to select the correct one, but equation (*) is sufficient to mock up a solution in a graphical tool such as GeoGebra.