This question asked:
What is the probability that three points selected uniformly randomly on the unit circle contain a fixed point at distance $x$ from the circle's centre?
I answered that question with a geometric derivation of the following double integral for the desired probability: $$P(x)=\frac14-\frac3{\pi^3}\int_0^\pi\int_0^a\left(\sin^{-1}\frac{x\sin b}{\sqrt{1+x^2-2x\cos b}}-\sin^{-1}\frac{x\sin a}{\sqrt{1+x^2-2x\cos a}}\right)\,db\,da$$ Below this equation I claimed:
Trying to find a closed-form expression for this is neither simple nor enlightening.
I did give an approximation to $P(x)$ and showed that it had an error of no more than around 0.004 via matplotlib. (In the graphs below, the pole refers to the fixed point.)
$$P(x)\approx\frac{(1-x^2)^{2/3}}4$$
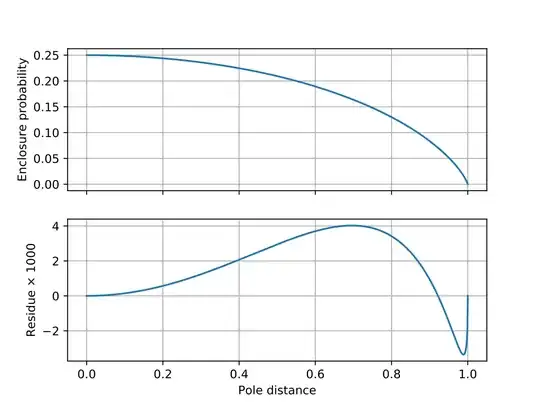
But the relative size of the error irritated me – I had tried more complicated approximations, with only marginal improvements. Then I got the idea of using Taylor series for a better approximation – $P(x)$ is only defined on $[0,1]$, within the radius of convergence for many Taylor series.
So I set to work, using SymPy to compute the Maclaurin (Taylor at $x=0$) series of $P(x)$. After half an hour I got the following: $$P(x)=\frac14-\frac{3x^2}{2\pi^2}-\frac{3x^4}{8\pi^2}-\frac{x^6}{6\pi^2}-\frac{3x^8}{32\pi^2}-\frac{3x^{10}}{50\pi^2}+\mathcal O(x^{12})$$ I realised that
- the initial term and the factors of $\frac3{\pi^2}$ in subsequent terms were echoes of their presence in the expression for $P(x)$, so could be factored out
- computing the $x^{12}$ term would take forever in this form, so I split the integrand into four parts using the logarithmic version of $\sin^{-1}$: $$\int_0^\pi\int_0^a\left(\sin^{-1}\frac{x\sin b}{\sqrt{1+x^2-2x\cos b}}-\sin^{-1}\frac{x\sin a}{\sqrt{1+x^2-2x\cos a}}\right)\,db\,da=\\ i\left(\int_0^\pi\int_0^a\ln(xe^{ib}-1)\,db\,da-\frac12\int_0^\pi\int_0^a\ln(1+x^2-2x\cos b)\,db\,da\\ -\int_0^\pi\int_0^a\ln(xe^{ia}-1)\,db\,da+\frac12\int_0^\pi\int_0^a\ln(1+x^2-2x\cos a)\,db\,da\right)\tag1$$
With that, I computed the $x^{12}$ term: $$P(x)=\frac14-\frac3{\pi^2}\left(\frac{x^2}2+\frac{x^4}8+\frac{x^6}{18}+\frac{x^8}{32}+\frac{x^{10}}{50}+\frac{x^{12}}{72}+\mathcal O(x^{14})\right)$$ All the powers were even and had unit fraction coefficients after factoring $\frac3{\pi^2}$ out. I then put the sequence $2,8,18,32,50,72$ into the OEIS and got a surprise… these are twice squares!
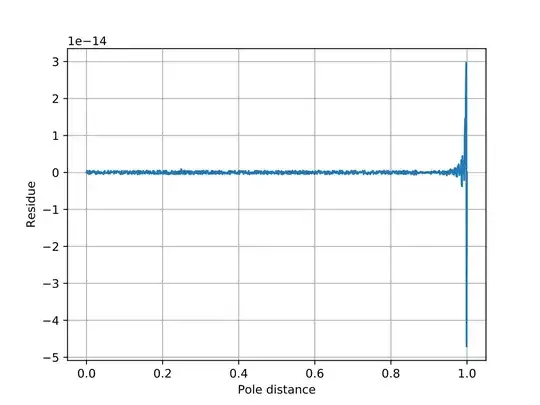
Therefore I could write $$P(x)=\frac14-\frac3{\pi^2}\sum_{n=1}^\infty\frac{x^{2n}}{2n^2}$$ Thus was revealed the series expansion of the dilogarithm, the simplest expression for $P(x)$ and perhaps the most elegant equation I have encountered: $$\bbox[5px,border:1px solid black]{P(x)=\frac14-\frac3{2\pi^2}\operatorname{Li}_2(x^2)}$$ I confirmed the correctness of this expression by comparing its values to my precomputed samples of $P(x)$, finding nothing but round-off error in the latter:
Of course, such an equality begs explanation, and this is the question I am asking here:
Why is the following identity true? $$\int_0^\pi\int_0^a\left(\sin^{-1}\frac{x\sin b}{\sqrt{1+x^2-2x\cos b}}-\sin^{-1}\frac{x\sin a}{\sqrt{1+x^2-2x\cos a}}\right)\,db\,da=\frac\pi2\operatorname{Li}_2(x^2)$$
The logarithmic form $(1)$ of the integrand in $P(x)$ may help. Besides Taylor series, I am open to proofs that exploit the geometry of the situation; here is the diagram I used to justify the integral expression for $P(x)$.
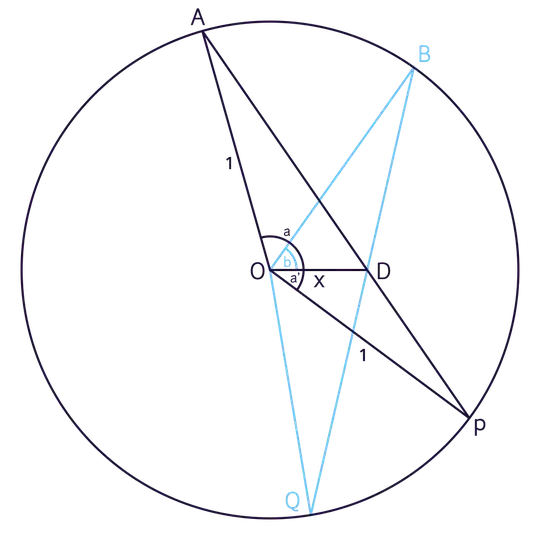
Here $O$ is the origin and the arguments of $A$ and $B$ when treated as complex numbers are $a$ and $b$, lying in $[0,\pi]$ and $[0,a]$ respectively. The argument of the triangle's third point (not shown) lies in $[-\pi,0]$ and has to be between $P$ and $Q$ for the triangle to contain the fixed point $D$ at $(x,0)$. The first term in the integrand $\sin^{-1}\frac{x\sin b}{\sqrt{1+x^2-2x\cos b}}$ is $\angle DOQ$, the second term $\angle DOP$.