1

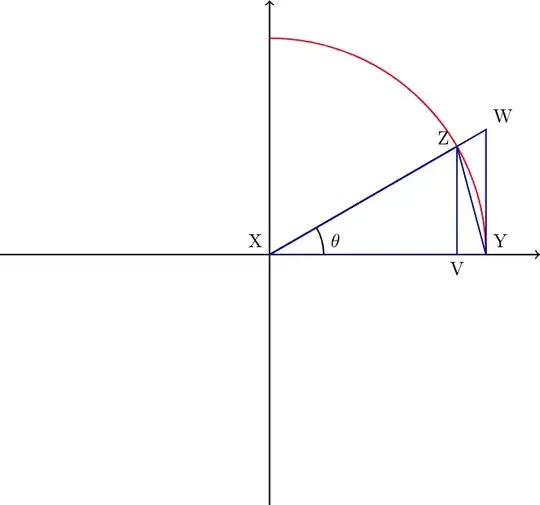
Archimedes used the fact that

$\sin(x)< x< \tan(x)$ when $0< x < \cfrac{\pi}2$

to prove that the perimeter of a polygon inscribed in a circle is less than the circumference of the circle. Similarly, he used this to show that the perimeter of a polygon circumscribed about a circle exceeds the circumference of the circle. I want to get some idea as to how Archimedes proved the above result.

Yash Jain
  • 1
k13
  • 259
  • Maybe just plot the graph? – D F Feb 07 '18 at 05:52
  • Look at $f(x)=\sin x-x$ and $g(x)=x-\tan x$. Using calculus it's easy to see these inequalities are true: $f'(x) \lt 0$ and $g'(x) \lt 0$ for $x\lt \frac {\pi}2$, with $f(0)=g(0)=0$... –  Feb 07 '18 at 06:09
  • Archimedes had techniques equivalent to modern day calculus... but i have no idea how he established these inequalities... Remember he was one of the four greatest ever. (Euler, Gauss and Newton being the other three...) –  Feb 07 '18 at 06:15
  • See my answer here for example. – dxiv Feb 07 '18 at 06:54
  • @ChrisCuster - "Archimedes had techniques equivalent to modern day calculus", really? care to back that statement up? – Nathaniel Bubis Feb 07 '18 at 10:49
  • I'm referring to his use of the "method of exhaustion ", if nothing else. .. https://en.m.wikipedia.org/wiki/Method_of_exhaustion –  Feb 07 '18 at 20:15
  • @nbubis. Maybe a more accurate statement would be that he had begun to discover the principles of calculus... –  Feb 07 '18 at 20:39

1 Answers1

3

Consider the following triangles in the unit circle: enter image description here

We know the following: $\overline{XY} =\overline{XZ} = 1$, $\overline{XV} = \cos\theta$, $\overline{ZV} = \sin\theta$, $\overline{WY} = \tan\theta$. Now, the area of the triangle $\Delta XZY$ is obviously $\frac{1}{2}\sin\theta$. The area of the sector of the unit circle containing $\Delta XZY$ is $\frac{1}{2}\theta$. Finally, the area of $\Delta XWY$ is $\frac{1}{2}\tan\theta$. Since $\Delta XWY$ contains the sector, which contains $\Delta XZY$, we have: $$\frac{1}{2}\sin\theta < \frac{1}{2}\theta < \frac{1}{2}\tan\theta$$ It is easy to go from this to $$\sin\theta < \theta < \tan\theta$$

bames
  • 2,106
  • 1
  • 8
  • 15