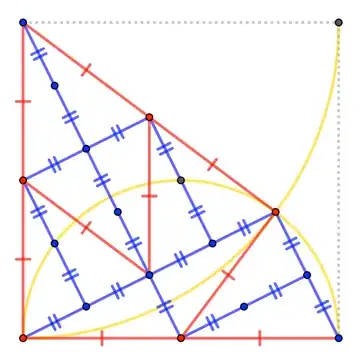
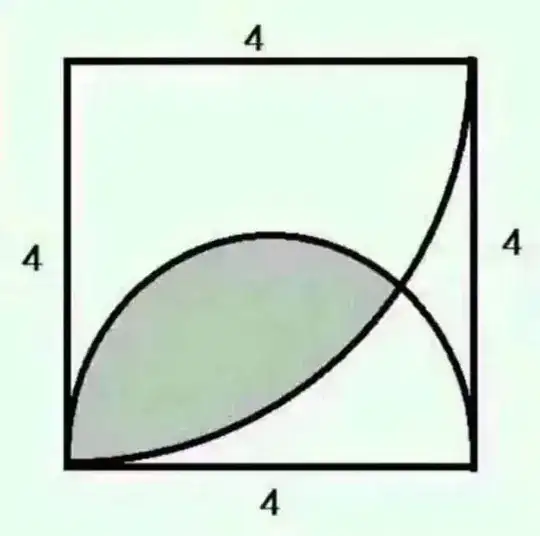
How to find the shaded area

Question

How to find the shaded area crossed by semi-circle of radius 2 and quarter-circle of radius 4?

I have 2 arctan(2)4pi - 8/5 + 2 arctan(1/2)16pi - 32/5. However arctan(2) and arctan(1/2) are not rational multiple of pi. And this question is supposed to be an elementary school math question, so the answer should be in terms of pi, without trigonometry. — Ed Zeng, Feb 06 '18 at 06:14

score 6 · Answer 1 · answered Feb 07 '18 at 00:05

6

The shaded area is shaped from two intersecting circles like an asymmetric lens! in order to find the area of this lens we simply split it in two parts:

answered Feb 07 '18 at 00:05

Seyed

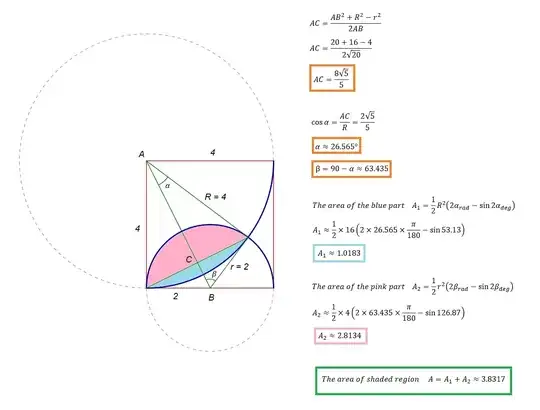
8,933

Thanks! What software do you use to draw such nice diagrams? – Ed Zeng Feb 07 '18 at 05:32
1

@EdZeng, I use C.a.r which is for free. Here is it's address:http://car.rene-grothmann.de/doc_en/download.html – Seyed Feb 07 '18 at 11:26

Blue · Answer 2 · 2018-02-07T08:29:20.683

5

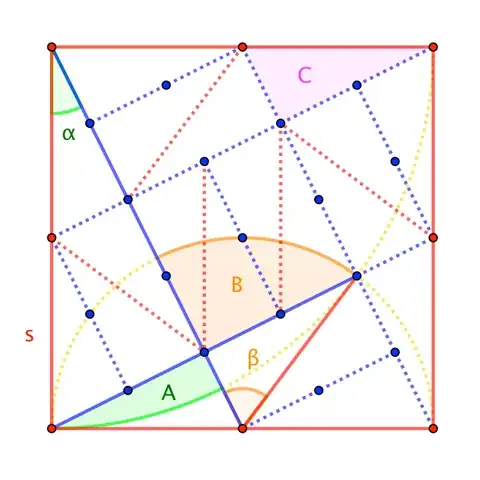
Hint.

(This space intentionally left blank.)

Solution.

$$\begin{align} \frac12\cdot\text{target area} &= A + B \\ &= \left( \frac12 \cdot (2s)^2\cdot\alpha - 4 C\right) + \left(\frac12 \cdot s^2 \cdot \beta - C \right) \\[4pt] &= \frac12 s^2\left( 4 \alpha + \beta \right) - 5 C \\[4pt] &=\frac12 s^2 \left( \frac\pi2 + 3\alpha \right)-5 \cdot \frac{1}{20}(2s)^2 \\[4pt] &= \frac12 s^2 \left( \frac\pi2 + 3\operatorname{atan}\frac{1}{2} - 2 \right) \end{align}$$ So, the target area, with $s = 2$, is

$$2 \pi + 12 \operatorname{atan}\frac{1}{2} - 8 $$

edited Feb 07 '18 at 08:29

answered Feb 06 '18 at 08:08

Blue

75,673

Thanks! I am not sure how to find the area of the arc without using trigonometry though. BTW, what software do you use to draw such nice diagram? – Ed Zeng Feb 07 '18 at 05:30
@EdZeng: The answer must include an inverse-trig function somewhere, since, as you note, the angles involved are necessarily non-rational multiples of $\pi$. (For reference, this question addresses that issue directly: "ArcTan(2) a rational multiple of $\pi$?".) If this is an "elementary school math question", then those kids must be pretty bright! :) (BTW: I use GeoGebra for my diagrams.) – Blue Feb 07 '18 at 08:38

user5713492 · Answer 3 · 2018-02-06T07:50:36.970

4

This problem is so funny. @Robert Z's first answer of $$4\sin^{-1}\left(\frac2{\sqrt5}\right)+8\sin^{-1}\left(\frac45\right)-8$$ was correct as is his latest answer of $$4\left(\pi-2-\tan^{-1}\left(\frac2{11}\right)\right)$$ Integrating in polar coordinates I got $$12\tan^{-1}\left(\frac12\right)-8+2\pi$$ Which was also correct. Taking the difference between sectors of circles and triangles, I get $$16\sin^{-1}\left(\frac1{\sqrt5}\right)-8+4\sin^{-1}\left(\frac2{\sqrt5}\right)$$ Amazing that all $4$ of these expressions are the same! Even $$8\pi-12\tan^{-1}2-8$$ As was seen in two nearly simultaneous answers was OK. How about sticking to Pythagorean triples with $$6\sin^{-1}\left(\frac45\right)+2\pi-8$$

edited Feb 06 '18 at 07:50

answered Feb 06 '18 at 07:15

user5713492

15,938

I found another equivalent answer (with no fractions) which is the similar to the one you obtained by polar coordinate. – Robert Z Feb 06 '18 at 07:33
@Robert Z I don't know why you deleted your post -- you had Michael Rozenberg beat by a couple of minutes :) – user5713492 Feb 06 '18 at 07:45

score 1 · Answer 4 · answered Feb 06 '18 at 07:35

Let $ABCD$ be our square, where $B$ is a center of the circle with the radius $4$ and $AD$ is a diameter of the second circle.

Let these circles be intersected in points $A$ and $E$ and $G$ be the center of the second circle.

Thus, the needed area it's: $$\frac{1}{2}\cdot4^2\cdot2\arctan\frac{1}{2}+\frac{1}{2}\cdot2^2\cdot2\arctan2-S_{ABEG}=$$ $$=16\arctan\frac{1}{2}+4\arctan2-4\cdot2=$$ $$=16\left(\frac{\pi}{2}-\arctan2\right)+4\arctan2-4\cdot2=8\pi-12\arctan2-8.$$

How to find the shaded area

4 Answers4

Linked