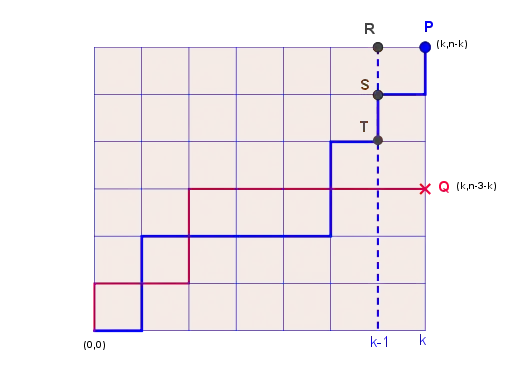
Reading through my textbook I came across the following problem, and I am looking for some help solving it. I am asked to prove the following by two different methods, one combinatorial and one algebraic. If I could get help with either or both it would be great, thanks!
Prove that this identity is true,
$$\binom{n}{k} -\binom{n-3}{k} =\binom{n-1}{k-1} + \binom{n-2}{k-1} + \binom{n-3}{k-1}$$
Combinatorial: Rearrange to $${n\choose k}={n-1\choose k-1}+{n-2\choose k-1}+{n-3\choose k-1}+{n-3\choose k}$$
Choose $k$ objects out of $\{1,2,\ldots, n\}$. This is counted by LHS. We can also partition such choices into four parts:
(a) $1$ is the smallest item in our set of $k$.
(b) $2$ is the smallest item in our set of $k$.
(c) $3$ is the smallest item in our set of $k$.
(d) Our set of $k$ contains none of $\{1,2,3\}$.
The four terms of the RHS count just these four cases.
Hint: Put $\binom{n-3}{k}$ to the other side and collect terms.
This way we obtain starting with the right-hand side \begin{align*} &\binom{n-1}{k-1}+\binom{n-2}{k-1}+\color{blue}{\binom{n-3}{k-1}+\binom{n-3}{k}}\\ &\qquad=\binom{n-1}{k-1}+\color{blue}{\binom{n-2}{k-1}+\binom{n-2}{k}}\\ &\qquad=\color{blue}{\binom{n-1}{k-1}+\binom{n-1}{k}}\\ &\qquad=\color{blue}{\binom{n}{k}} \end{align*}
Repeatedly, use the identity (Pascal's Identity), namely $$ \binom{n}{k}=\binom{n-1}{k}+\binom{n-1}{k-1}. $$ Note that $$ \left(\binom{n}{k}-\binom{n-1}{k-1}\right)-\binom{n-2}{k-1}-\binom{n-3}{k-1}-\binom{n-3}{k} $$ equals $$ \binom{n-1}{k}-\binom{n-2}{k-1}-\binom{n-3}{k-1}-\binom{n-3}{k} $$ which equals $$ \binom{n-2}{k}-\binom{n-3}{k-1}-\binom{n-3}{k} $$ which equals $$ \binom{n-3}{k}-\binom{n-3}{k}=0 $$ as desired.
The following algebraic approach is some sort of overkill and for curiosity only. We use the coefficient of operator $[x^n]$ to denote the coefficient of $x^n$ in a series. This way we can write for instance \begin{align*} \binom{n}{k}=[x^k](1+x)^n \end{align*}
We start with the left-hand side and obtain \begin{align*} \color{blue}{\binom{n}{k}-\binom{n-3}{k}}&=[x^k]\left((1+x)^n-(1+x)^{n-3}\right)\\ &=[x^k]\left((1+x)^3-1\right)(1+x)^{n-3}\\ &\color{blue}{=[x^k](x^3+3x^2+3x)(1+x)^{n-3}}\tag{1} \end{align*}
The right-hand side admits the representation \begin{align*} \color{blue}{\binom{n-1}{k-1} }&\color{blue}{+ \binom{n-2}{k-1} + \binom{n-3}{k-1}}\\ &=[x^{k-1}]\left((1+x)^{n-1}+(1+x)^{n-2}+(1+x)^{n-3}\right)\\ &=[x^{k-1}]\left((1+x)^2+(1+x)+1\right)(1+x)^{n-3}\\ &=[x^{k-1}]\left(x^2+3x+3\right)(1+x)^{n-3}\\ &\,\,\color{blue}{=[x^k]\left(x^3+3x^2+3x^2\right)(1+x)^{n-3}}\tag{2}\\ \end{align*}
Since (1) and (2) coincide the claim follows.
Combinatorial proof without words:
\begin{align*} \hline \end{align*}
Or with some words:
We consider the lattice paths of length $n$ from $(0,0)$ to $(k,n-k)$ consisting of $(1,0)$-steps and $(0,1)$-steps only. The number of these paths is $$\binom{n}{k}$$ since we have to choose precisely $k$ $(1,0)$-steps out of $n$ steps.
The identity \begin{align*} \underbrace{\binom{n}{k}}_{\color{blue}{\textbf{P}}} -\underbrace{\binom{n-3}{k}}_{\color{red}{\textbf{Q}}} =\underbrace{\binom{n-1}{k-1}}_{\textbf{R}} + \underbrace{\binom{n-2}{k-1}}_{\textbf{S}} + \underbrace{\binom{n-3}{k-1}}_{\textbf{T}} \end{align*} is valid, since
- the number of paths from $(0,0)$ to $\color{blue}{P=(k,n-k)}$ which do not pass $\color{red}{Q=(k,n-3-k)}$
is the same as the number of paths from $(0,0)$ which go either
to $R=(k-1,n-k)$
or $S=(k-1,n-1-k)$
or $T=(k-1,n-2-k)$.
Note: Each of the paths to $R,S,T$ can be uniquely extended to $P$ via a $(1,0)$-step followed by zero, one or two $(0,1)$ steps.
For the combinatorial approach, consider the following problem: you have the first $n$ numbers $1,\dots,n$ and you want to pick $k$ of them in such a way that you pick at least one of $1$, $2$ or $3$. On the LHS you compute the total number of choices minus the choices in which you don't pick any of $1$,$2$ or $3$. On the RHS you sum over the cases in which you pick $1$ and another $k-1$ numbers, or $2$ and another $k-1$ numbers but NOT $1$, or $3$ and another $k-1$ numbers but NOT $1$ and $2$. So you have two different ways of counting the same thing.
Combinatorial: $k$ people are selected from a group of $n$, $1\le k\le n-3$. Choose $1$ leader and then the remaining $k-1$ people for a total of $k$ people chosen. There are $3$ candidates to choose from for the leader that each have a unique different level $1,2$ or $3$. Once a candidate is selected, no candidate with a lower level may be selected for the remaining $k-1$ people.
LHS: All possible selections minus the case where none of the candidates are selected.
RHS: Level 1 candidate chosen + level 2 candidate chosen + level 3 candidate chosen.
