I know that I should use the definition of an odd integer ($2k+1$), but that's about it.
Thanks in advance!
I know that I should use the definition of an odd integer ($2k+1$), but that's about it.
Thanks in advance!
Step 1: pick an odd number (like $n=13$ here)

Step 2: bend it in "half" (any odd number $n$ can be written as $2k+1$, and $13=2\cdot 6 + 1$)
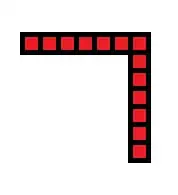
Step 3: fill in the blank space

Step 4: Count squares. (Here, the blue square has area $36=6^2$, while the whole square has area $49=7^2$)
Hint: Consider the difference of two consecutive squares. What is $(k+1)^2-k^2$?
HINT: $$\begin{align} &2k + 1 \\= & 1\cdot(2k + 1) \\ =& \left(k + 1 - k \right)\left(k + 1 + k\right) \\ = & \cdots\end{align}$$
Here is a more calculational answer where we try to 'construct' the solution by minimizing the amount of 'magic' in the proof. I'm assuming all variables are integers.
Given an odd $\;n\;$, we are asked to find $\;a,b\;$ such that $$ a^2 - b^2 = n $$
Let's calculate: \begin{align} & a^2 - b^2 = n \\ \equiv & \;\;\;\;\;\text{"arithmetic -- the simplest thing I know about the difference of squares"} \\ & (a+b) \times (a-b) = n \\ \equiv & \;\;\;\;\;\text{"arithmetic -- the simplest thing to give both sides similar structure"} \\ & (a+b) \times (a-b) = n \times 1 \\ \Leftarrow & \;\;\;\;\;\text{"logic: Leibniz -- the simplest thing to exploit the structural similarity"} \\ & a+b = n \;\land\; a-b = 1 \\ \equiv & \;\;\;\;\;\text{"arithmetic: solve for $\;a,b\;$"} \\ & a = (n+1)/2 \;\land\; b = (n-1)/2 \\ \end{align} Now since $\;n\;$ is odd, both $\;(n+1)/2\;$ and $\;(n-1)/2\;$ are integers, and therefore we have found the required $\;a,b\;$.
a + b = n and a - b = 1 follows from (a+b)×(a−b)=n×1.
– mcandre
Jan 02 '16 at 02:12
f(a, b) = f(c, d) has solutions where (c, d) != (a, b). Is multiplication special this way?
Would a + b = 1 and a - b = n also have integer solutions, since n*1 = 1*n?
The algebraic equivalent of orlandpm's very elegant illustration is this:
Let a be any integer . . .
$K = (a+1)^2 - a^2$
$K = (a^2 + 2a + 1) - a^2$
$K = a^2 + 2a + 1 - a^2$
$K = 2a + 1$, which defines any odd integer; Q.E.D.
$s around your formulas)
– xavierm02
Jul 27 '13 at 23:59
To get the complete classification of differences of Thai squares, we use the elementary observation that $a^2-b^2=(a+b)(a-b)$.
Clearly, $a+b$ and $a-b$ at either both even or both odd. So a d difference of two squares is either of our a multiple of $4$.
In fact, if $N$ is odd or a multiple of $4$, then we can always find $a$, $b$ such that $N=a^2-b^2$: if $N$ is odd, take $a=(N+1)/2$ and $b=(N-1)/2$, and if $N$is sa multiple of $4$, take $a=N/2+1$ and $b=N/2-1$.
Eric and orlandpm already showed how this works for consecutive squares, so this is just to show how you can arrive at that conclusion just using the equations.
So let the difference of two squares be $A^2-B^2$ and odd numbers be, as you mentioned, $2k+1$. This gives you $A^2-B^2=2k+1$.
Now you can add $B^2$ to both sides to get $A^2=B^2+2k+1$. Since $B$ and $k$ are both just constants, they could be equal, so assume $B=k$ to get $A^2=k^2+2k+1$. The second half of this equation is just $(k+1)^2$, so $A^2=(k+1)^2$, giving $A = ±(k+1)$, so for any odd number $2k+1$, $(k+1)^2-k^2=2k+1$.
You could add.
For mod ((2x+1),4)= 1, 2x+1 has at least one more solution than (k^2+1)-k^2=2x+1 and k^2 will be odd and (k-n)^2 will be even. Opposite if Mod((2x+1),4)= 3. n is always odd.
k^2-(k+n)^2= 2x+1, if 2x+1 is a composite number, if not, 2x+1 only has the solution (k^2+1)-k^2=2x+1 and 2x+1 is a prime number.
Sorry Mathjax is not working on my computer.
Proof for odd numbers: Divide any odd number, $x$, in half, then let $C$ be the half rounded up and $B$ be the half rounded down. Then, $C^2 - B^2 = x$. Let's examine this algebraically:
$$C = \frac{x+1}{2}$$ $$B = \frac{x-1}{2}$$ $$C^2 - B^2 = \biggl(\frac{x+1}{2}\biggr)^2 - \biggl(\frac{x-1}{2}\biggr)^2 = \frac{x^2+2x+1}{4} - \frac{x^2-2x+1}{4} = \frac{x^2-x^2+2x+2x+1-1}{4} = \frac{4x}{4} = x$$
Then, because even/odd integers alternate, $x \pm 1$ will always result in an even integer when $x$ is odd and an odd integer when $x$ is even.
Because only even integers are divisible by two (without incurring a decimal), $x \pm 1$ must be even to be divisible by 2, so $x$ must be odd. Otherwise, if $x$ were even, then $C$ and $B$ would not be integers.
Example for odd numbers: Take the number 31. Let $C=\frac{31+1}{2}=16$ and $B=\frac{31-1}{2}=15$. Then, $16^2 - 15^2 = 256 - 225 = 31$.
Proof for all composite numbers: every pair of $x$'s factors, $p$ and $q$, including composite factor pairs, where the oddity of $p$ matches the oddity of $q$, corresponds to a separate representation as the difference of two squares:
$$p \times q = x$$
$$C = \frac{p + q}{2}$$
$$B = \frac{|p - q|}{2}$$
$$C^2 - B^2 = \biggl( \frac{p + q}{2} \biggl)^2 + \biggl( \frac{|p - q|}{2} \biggl)^2 = \frac{p^2 + 2pq + q^2}{4} - \frac{p^2 - 2pq + q^2}{4} = \frac{p^2 - p^2 + q^2 - q^2 + 4pq}{4} = pq = x$$
Example for every-other even numbers: Because half of every-other even number (that is, 4, 8, 12, etc.) has an even oddity, it can be shown that at least every-other even number can be expressed as the difference of two squares. For $x=48$, we get $p=2$ and $q=\frac{x}{p}=24$. Then, $C=\frac{2+24}{2}=13$ and $B=13-2=11$. We verify $C^2 - B^2 = 169 - 121 = 48$.
Conclusion: The only numbers that cannot be expressed as the difference of two squares are the sequence $4n+2$: 2, 6, 10, 14, 18, 22, etc.