If we are speaking of undistinguishable balls into distinguishable bins, as it is the common understanding
from the wording of your problem, then yes that article and the formula you cite is fully correct.
However I suggest to rewrite the formula as
$$
N_b (s,r,m)\quad \left| {\;0 \leqslant \text{integers }s,m,r} \right.\quad = \sum\limits_{\left( {0\, \leqslant } \right)\,\,k\,\,\left( { \leqslant \,\frac{s}
{r}\, \leqslant \,m} \right)} {\left( { - 1} \right)^k \left( \begin{gathered}
m \hfill \\
k \hfill \\
\end{gathered} \right)\left( \begin{gathered}
s + m - 1 - k\left( {r + 1} \right) \\
s - k\left( {r + 1} \right) \\
\end{gathered} \right)}
$$
with
$$N_{\,b} (s,r,m) = \text{No}\text{. of solutions to}\;\left\{ \begin{gathered}
0 \leqslant \text{integer }x_{\,j} \leqslant r \hfill \\
x_{\,1} + x_{\,2} + \cdots + x_{\,m} = s \hfill \\
\end{gathered} \right.$$
or No. of ways to distribute $s$ undist. balls into $m$ dist. bins, each of capacity max $r$ balls.
The advantages of this formulation are extensively described in this related post
and in this other one.
Coming now to the number of ways in which at least $q$ bins remain empty, your approach is not correct.
In fact (allow me to keep the symbols above)
that number is not given by $ N_{\,b} (s,r,m-q)$, because you shall multiply by the number of ways to insert the $q$ empty bins and this in turn
depends on how many empty bins are already accounted by $ N_{\,b} (s,r,m-q)$.
Taking the case of exactly $q$ empty bins, the No. of ways to obtain them
will be
No. of ways to choose $q$ bins out of $m\quad \quad \quad \times$
No. of ways to put the $s$ balls into the remaining $m-q$ bins, each filled with at least one ball
as in this formulation the two type of bins (empty/non-empty) are separated.
Since
$$
{\rm No}{\rm .}\,{\rm of}\,{\rm sol}{\rm .}\,{\rm to}\;\left\{ \matrix{
{\rm 1} \le {\rm integer}\;x_{\,j} \le r \hfill \cr
x_{\,1} + x_{\,2} + \; \cdots \; + x_{\,m} = s \hfill \cr} \right.\quad = \quad {\rm No}{\rm .}\,{\rm of}\,{\rm sol}{\rm .}\,{\rm to}\;\left\{ \matrix{
0 \le {\rm integer}\;\left( {x_{\,j} - 1} \right) \le r - 1 \hfill \cr
\left( {x_{\,1} - 1} \right) + \left( {x_{\,2} - 1} \right) + \; \cdots \; + \left( {x_{\,m} - 1} \right) = s - m \hfill \cr} \right.
$$
then clearly it is
$$
N_{be} (s,r,m,q) = \left( \matrix{
m \cr
q \cr} \right)N_b (s - m + q,r - 1,m - q)\quad \left| \matrix{
\;s < 0\; \vee \;r < 0\; \vee \;m < 0\;\; \Rightarrow \;N_b (s,r,m) = 0 \hfill \cr
\;1 \le s \hfill \cr} \right.\quad
$$
where the limit cases ($m=0$ etc.) shall be treated properly.
The "sprout" example that you cite in your comment perfectly fits with this model, if sprouting of one
seed in one compartment is independent from the sprouting of the other seeds in the same or in other compartment,
apart from having then a total of $k$.
Just allow to replace your $k$ with $s$, and we can apply the formula above
$$
\eqalign{
& N_{be} (s,r,m,q) = \left( \matrix{
m \cr
q \cr} \right)N_b (s - m + q,r - 1,m - q) = \cr
& = \left( \matrix{
m \cr
q \cr} \right)\sum\limits_{\left( {0\, \le } \right)\,\,k\,\,\left( { \le \,{s \over r}\, \le \,m} \right)} {\left( { - 1} \right)^k \left( \matrix{
m - q \cr
k \cr} \right)\left( \matrix{
s - 1 - kr \cr
s - m + q - kr \cr} \right)} \cr}
$$
To make a small numerical example, with $s=3,\; m=3,\; r=2$
$$
\eqalign{
& N_{be} (3,2,3,q) = \left( \matrix{
3 \cr
q \cr} \right)\sum\limits_{\left( {0\, \le } \right)\,\,k\,\,\left( { \le \,1} \right)} {\left( { - 1} \right)^k \left( \matrix{
3 - q \cr
k \cr} \right)\left( \matrix{
2 - 2k \cr
0 + q - 2k \cr} \right)} = \cr
& = \left( \matrix{
3 \cr
q \cr} \right)\left( {\left( \matrix{
3 - q \cr
0 \cr} \right)\left( \matrix{
2 \cr
q \cr} \right) - \left( \matrix{
3 - q \cr
1 \cr} \right)\left( \matrix{
0 \cr
q - 2 \cr} \right)} \right) = \cr
& = \left( \matrix{
3 \cr
q \cr} \right)\left( {\left( \matrix{
2 \cr
q \cr} \right) - \left[ {q = 2} \right]} \right) = \underbrace {1,6,0,0}_{q\, = \,0 \cdots 3}\quad \Rightarrow \cr
& \Rightarrow \quad \left\{ \matrix{
\underbrace {(1,1,1)}_{{\rm 3}\,{\rm boxes}\,{\rm content}}\quad q = 0 = {\rm no}\,{\rm empty} \hfill \cr
{\rm permut}{\rm .}\,{\rm of}\;(0,1,2) = 6\quad q = 1 = {\rm one}\,{\rm empty} \hfill \cr
\emptyset \quad q = 2,3 \hfill \cr} \right. \cr}
$$
------- notes for computation -------
a) you need first of all a computer program which include the binomial defined as in this wiki article, i.e.
$$
\left( \matrix{
x \cr
m \cr} \right) = \left\{ {\matrix{
{{{x^{\,\underline {\,m\,} } } \over {m!}} = {1 \over {m!}}\prod\limits_{0\, \le \,k\, \le \,m - 1} {\left( {x - k} \right)} } & {0 \le m \in Z} \cr
0 & {m < 0\; \vee \;m \notin Z} \cr
} } \right.
$$
because, either you have to adjust the bounds of the sum in a complicated way prone to errors, or you get an error for negative factorial.
If you don't have, it is not difficult to implement a "user defined function" accordingly.
The proposed formulations take advantage of the fact that, in the definition above, the binomial is null for lower term $<0$.
b) Take the formula above, for the number of ways to get exactly $q$ empty bins
$$
N_{be} (s,r,m,q) = \left( \matrix{
m \cr
q \cr} \right)\sum\limits_{0\, \le \,\,k\,\, \le \,m} {\left( { - 1} \right)^k \left( \matrix{
m - q \cr
k \cr} \right)\left( \matrix{
s - 1 - kr \cr
s - m + q - kr \cr} \right)}
$$
for computation purposes, you can fix the summation bounds to be simply $0 \le k \le m$.
The number of ways to get at least $q$ empty bins will clearly be
$$
\sum\limits_{q\, \le \,\,j\,\, \le \,m} {N_{be} (s,r,m,j)}
$$
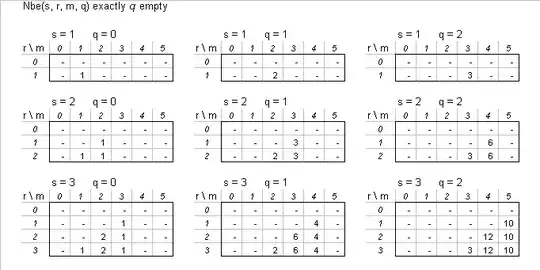
example
For the very few lowest values of the parameters the attached are the values
that we get applying the formula for $N_{be}$ given above.
You can verify that they are correct.