6

Introduction:

Recently I found out that $i^i \approx 0.20788$ has no imaginary part. I got interested and then wanted to know whether there are other $n$ for which $\underbrace {i^{i^{i^{.^{.^{.^{i}}}}}}}_{n \ times}$ has no inaginary part.

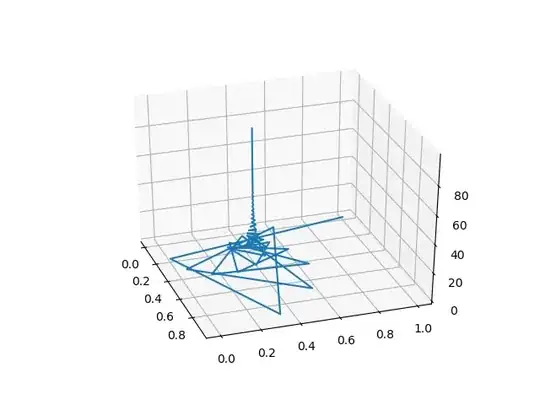
So I wrote this python script (I'm a beginner at python, could be very bad code :) which plots what I call the $i-Tower\ up\ to\ n = 100$. It looks like this: iTower

Question:

Let's use this convention: ${}^ni = \underbrace{i^{i^{i^{.^{.^{.^{i}}}}}}}_{n \ times}$.

  • Why is the sequence ${}^ni\ |\ n \in \mathbb{N}$ converging?

${}^{20}i \approx 0.48770 + 0.41217i$

${}^{60}i \approx 0.437584 + 0.360535i$

${}^{100}i \approx 0.43829+ 0.36059i$

What I already noticed is that the angle between the lines you can draw from ${}^ni$ over ${}^{n+1}i$ to ${}^{n+2}i$ is $<90°$.

  • Is that angle equal for all $n$?

  • Is there a way to give the exact value of $x = {}^ni \ $with$\ {n \rightarrow \infty}$?

  • What is the connection between $i$ and $x$. Is $x$ a special complex number that is maybe already known or comes up in other places?

Tweakimp
  • 165
  • I think the same question has been already asked by someone. – Rohan Shinde Jan 24 '18 at 13:50
  • 1
    See "Shell-Thron-region" (for area of convergence for complex bases $z$) The hint to Euler and Eisenstein by @JanEerland covers only real $z$ and to generalize this question to the complex numbers has not been trivial... – Gottfried Helms Jan 24 '18 at 16:58

1 Answers1

5
  • The infinite power tower converges to the value:

$$i^{i^{i^{\cdot^{\cdot^{\cdot^{\cdot}}}}}}=-\frac{\text{W}(-\ln(i))}{\ln(i)}=\frac{2\text{W}\left(-\frac{\pi i}{2}\right)i}{\pi}\approx0.438286+0.3605924i\tag1$$

See: MathWorld

  • Solving this equation:

$$a^b=b\Longleftrightarrow b=-\frac{\text{W}(-\ln(a))}{\ln(a)}\tag2$$

With $\text{W}(z)$ is the product log fuction

Notice, for the 'Product Log Function' (or the Lambert $\text{W}$-function) is defined as follows:

$$f(z)=ze^z\to z=f^{-1}(ze^z)=\text{W}(ze^z)\tag3$$

Now, we know that for $k\in\mathbb{R}^+$ (real, and bigger than zero) $\ln(k)$ is well defined.

Now, your question is about:

$$y(k)=k^{k^{k^{k^{\dots}}}}=-\frac{\text{W}\left(-\ln(k)\right)}{\ln(k)}\tag4$$

Eisenstein's (1844) considered this series of the infinite power tower. $y(k)$ converges iff $e^{-e}\le k\le e^{\frac{1}{e}}$; OEIS A073230 and A073229), as shown by Euler (1783) and Eisenstein (1844) (Le Lionnais 1983; Wells 1986, p. 35).

So, the domain of $y(k)$:

$$\left[0,e^{\frac{1}{e}}\right]\tag5$$

Jan Eerland
  • 28,671