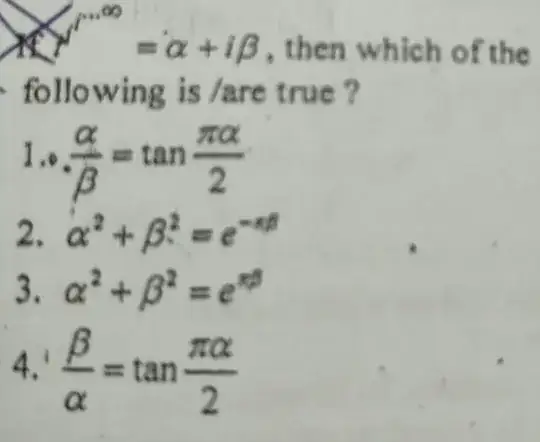Every level of exponentiation is multi-valued. Suppose we always pick the branch $i=e^{i\pi/2}$ in every level. Then we have
$$(e^{i\pi/2})^{\alpha+i\beta}=e^{-\pi\beta/2}\left(\cos\frac{\pi\alpha}{2}+i\sin\frac{\pi\alpha}{2}\right)=\alpha+i\beta.$$
Two simultaneous equations for real $\,\alpha\,$ and $\,\beta\,$ are established by comparing the real and imaginary parts. We have
$$\left\{\begin{array}{l}
e^{-\pi\beta/2}\cos\displaystyle\frac{\pi\alpha}{2}=\alpha,\\
\ \\
e^{-\pi\beta/2}\sin\displaystyle\frac{\pi\alpha}{2}=\beta.\\
\end{array}\right.$$
Therefore $\,\alpha^2+\beta^2=e^{-\pi\beta}\,$ and $\,\frac{\beta}{\alpha}=\tan\frac{\pi\alpha}{2}$ can be found without numerically solving for $\,\alpha\,$ and $\,\beta$. Their numerical values are given by $\,\alpha=0.4383\,$ and $\,\beta=0.3606$.