3

In the center of a rounded table with a radius of 50cm, there is a smaller circle with a radius of 10cm. A coin with a radius of 1cm is thrown on the table. Assuming that it will always land on the table, what is the probability that the entire coin will be inside the smaller circle?

To start with, I have plotted this situation using GeoGebra:

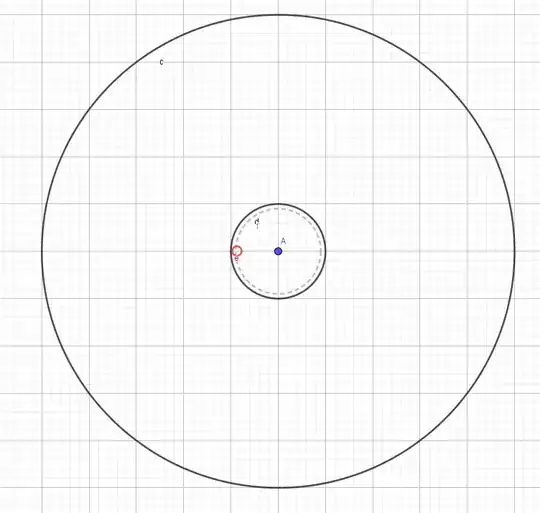
Since that coin has a radius of 1cm, I have plotted another circle with a radius of 9.

The area of the big table is $50^{2}\pi$ , while the areas of the smaller circles are $10^{2}\pi$ and $1^{2}\pi$ respectively.

My intuition say that the probability should be

$$\frac{9^{2}\pi}{50^{2}\pi} =0.0324$$

but I can't explain it. Am I correct ? What is the mathematical reasoning ?

Ѕᴀᴀᴅ
  • 34,263
Jankel
  • 85

2 Answers2

1

Your answer is correct. There are several layers of how much in-detail you want to go with how to mathematically explain the answer. A fairly basic (but, for most uses, sufficient) would be:

First, some observations:

  • the position of the coin is uniquely determined by the position of its center.
  • the coin lies entirely in the inner circle if and only if its center lies in a circle with radius $9$.
  • The coin lies on the table if and only if its center lies on the table.

We also make the implicit assumptions that All positions of the coin are equally likely

From these, we can conclude that the question can be rephrased as:

If we randomly pick one point of a circle with radius $50$, what is the probability that the point lies in an inner circle with radius $9$?

And the answer to that, as always in questions of the type "if we are in this area, what is the probability that we are in this sub-area" is simply the ratio of the surface area of the sub-area (in our case, the small circle) to the surface area of the entire area (in our case, the big circle), so

$$\frac{\pi 9^2}{\pi 50^2}$$

5xum
  • 123,496
  • 6
  • 128
  • 204
1

The center of the coin must fall inside a circle of area $\pi\,9^2$ while we know that it falls on a zone of area $\pi\,49^2$ of the table$^*$.

Hence

$$\frac{81}{2401}.$$

$^*$You could question if the coin must fall fully over the table or not, but in any case, falling with its center at radius $50$ wouldn't allow it to stay and the useful radius is smaller than $50$.