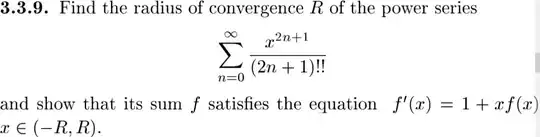Question If $\displaystyle f(x)=\sum_{n=0}^{\infty}\frac{x^{2n+1}}{(2n+1)!!}$ then prove that
$f'(x)=1+xf(x)$
Book's Question
I can prove its radius of convergence is infinity
Book's Answer
My Approach
$\displaystyle f(x)=\sum_{n=0}^{\infty}\frac{x^{2n+1}}{(2n+1)!!}$
$\displaystyle f'(x)=\sum_{n=1}^{\infty}\frac{(2n+1)x^{2n}}{(2n+1)!!}$
Now I cannot prove $f'(x)=1+xf(x)$
Hints:
In your derivation, what happens to the $n=0$ term? It is not a constant. In particular, for $n=0$, the corresponding term in $f$ is $\frac{x}{1!!}=x$, so its derivative is $1$.
Consider $\frac{2n+1}{(2n+1)!!}$. Since the double factorial is $$(2n+1)!!=(2n+1)(2n-1)(2n-3)\dots1,$$ the first factor of the double factorial cancels, leaving $(2n-1)!!$. Note that $!!$ does not mean taking the factorial twice.
If you are given a power series $$ f(x)=\sum_{n=0}^{\infty}a_nx^n $$ with positive (possibly infinite) radius of convergence, then in the interval of convergence $$ f'(x)=\sum_{n=1}^{\infty}na_nx^{n-1}\tag{*} $$ The shift in the starting index is done because $x^{n-1}$ would be wrong for $n=0$.
However, your series is not in the form (*), because it has no term for $x^0$, so we don't need to take care of it when differentiating term by term. Hence $$ f'(x)=\sum_{n=0}^{\infty}\frac{(2n+1)x^{2n}}{(2n+1)!!} $$ Now we can only simplify $$ \frac{2n+1}{(2n+1)!!}=\frac{1}{(2n-1)!!} $$ when $n>0$, so we have to detach the initial term: $$ f'(x)=1+\sum_{n=1}^{\infty}\frac{(2n+1)x^{2n}}{(2n+1)!!} =1+\sum_{n=1}^{\infty}\frac{x^{2n}}{(2n-1)!!} =1+x\sum_{n=1}^{\infty}\frac{x^{2n-1}}{(2n-1)!!} $$ with the shift $n=k+1$ we finally get $$ f'(x)=1+x\sum_{k=0}^{\infty}\frac{x^{2k+1}}{(2k+1)!!} =1+xf(x) $$
The definition of the semifactorial $m!!$ is $$ m!!= \begin{cases} 2\cdot 4\cdot \ldots \cdot m & \text{$m$ even} \\[4px] 1\cdot 3\cdot \ldots \cdot m & \text{$m$ odd} \end{cases} $$